Transcription
CAPÍTULO 5Análisis de Fourier deseñales y sistemasde tiempo continuo5.1INTRODUCCIÓNEn capítulos anteriores presentamos la transformada de Laplace y la transformada z para convertir las señales en eldominio del tiempo en representaciones en el dominio s y el dominio z complejos que son, para muchos propósitos,más convenientes para analizar y procesar. Además, mediante estas transformaciones se proporciona mayor conocimiento acerca de la naturaleza y las propiedades de muchas señales y sistemas. En este capítulo y en el siguientepresentaremos otras transformaciones conocidas como la serie de Fourier y la transformada de Fourier, las cualesconvierten señales en el dominio del tiempo en representaciones en el dominio de la frecuencia (o espectrales). Además de proporcionar las representaciones espectrales de las señales, el análisis de Fourier también es esencial paradescribir ciertos tipos de sistemas y sus propiedades en el dominio de la frecuencia. En este capítulo nos introduciremos en el análisis de Fourier en el contexto de las señales y sistemas de tiempo continuo.5.2REPRESENTACIÓN EN SERIE DE FOURIER DE SEÑALES PERIÓDICASA. SEÑALES PERIÓDICASEn el capítulo 1 definimos una señal de tiempo continuo x(t) como periódica si existe un valor positivo distinto decero T para el cual(5.1)x(t T ) x(t ) para toda tEl periodo fundamental T0 de x(t) es el valor positivo más pequeño de T para el cual la ecuación (5.1) se satisface, y1@T0 5 f0 se conoce como frecuencia fundamental.Dos ejemplos básicos de señales periódicas son la señal senoidal realx(t)cos( v0 tf)(5.2)y la señal exponencial complejax(t)e jv 0 t(5.3)donde v0 5 2p@T0 5 2pf0 se conoce como frecuencia angular fundamental.B. REPRESENTACIÓN DE LA SERIE DE FOURIER EXPONENCIAL COMPLEJALa representación de la serie de Fourier exponencial compleja de una señal periódica x(t) con periodo fundamentalT0 está dada por
5.2 REPRESENTACIÓN EN SERIE DE FOURIER DE SEÑALES PERIÓDICAShx (t )k ck e jkv0 tv0h2pT0153(5.4)donde ck se conocen como coeficientes complejos de Fourier y están dados por1T0ckµT0x (t ) ejkv0 t(5.5)dtdonde eT0 denota la integral sobre cualquier periodo y por lo regular se utilizan los intervalos 0 hasta T0 o 2T0@2 hastaT0@2 para la integración. Al establecer k 5 0 en la ecuación (5.5) tenemos quec0 !1T0µT0(5.6)x(t ) dtlo cual indica que c0 es igual al valor promedio de x(t) sobre un periodo.Cuando x(t) es real, entonces de la ecuación (5.5) se deriva que(5.7)c2k 5 *kdonde el asterisco indica el complejo conjugado.C. SERIE DE FOURIER TRIGONOMÉTRICALa representación de la serie de Fourier trigonométrica de una señal periódica x(t) con periodo fundamental T0 estádada porh2pa0(5.8)v0x (t )(ak cos k v0 t bk sen k v0 t ) 2 k 1T0donde ak y bk son los coeficientes de Fourier dados porak !2T0µTx (t ) cos k v0 t dt(5.9a)bk !2T0µTx (t ) sen k v0 t dt(5.9b)00Los coeficientes ak y bk y los coeficientes de Fourier complejos ck se encuentran relacionados por (problema 5.3)a02c0akckckbkj ( ck1( ak2jbk )c k)(5.10)De la ecuación (5.10) obtenemosck1( ak2jbk )ck(5.11)Cuando x(t) es real, entonces ak y bk son reales, y por la ecuación (5.10) tenemos queak2 Re[ ck ]bk2 Im[ ck ](5.12)SEÑALES PARES E IMPARESSi una señal periódica x(t) es par, entonces bk 5 0 y su serie de Fourier (5.8) contiene únicamente los términos coseno:h2pa0x (t )ak cos k v 0 tv0(5.13) 2 k 1T0Si x(t) es impar, entonces ak 5 0 y su serie de Fourier contiene sólo términos seno:hx (t ) ! bk sen k v0 tk !1v0 !2pT0(5.14)
154D.CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUOSERIE DE FOURIER EN FORMA ARMÓNICAOtra forma de la representación en serie de Fourier de una señal periódica real x(t) con periodo fundamental T0 eshx (t )C0 Ck cos( k v 0tuk )v0k 12pT0(5.15)La ecuación (5.15) puede derivarse de la ecuación (5.8) y se conoce como serie de Fourier en forma armónica de x(t).El término C0 se conoce como componente de cd, mientras que el término Ckcos(kv0t 2 uk) se denomina k-ésimacomponente armónica de x(t). La primera componente armónica C1 cos(v0t 2 u1) se conoce comúnmente como componente fundamental debido a que tiene el mismo periodo fundamental que x(t). Los coeficientes Ck y los ángulos ukson las amplitudes y los ángulos de fase de las armónicas, respectivamente, y están relacionados con los coeficientesde Fourier ak y bk por medio dea0buk tan 1 k(5.16)C0Ckak2 bk22akPara una señal periódica real x(t), la serie de Fourier en términos de exponenciales complejas como los de laecuación (5.4) es matemáticamente equivalente a cualesquiera de las dos formas en las ecuaciones (5.8) y (5.15).Aunque las últimas dos son formas comunes para la serie de Fourier, la forma compleja en la ecuación (5.4) es másgeneral y, por lo general, más conveniente; utilizaremos esa forma casi de manera exclusiva.E. CONVERGENCIA DE LA SERIE DE FOURIERSe sabe que una señal periódica x(t) tiene una representación en serie de Fourier si satisface las siguientes condiciones de Dirichlet:1. x(t) es absolutamente integrable sobre cualquier periodo; esto es,µT0x (t ) dt ! h(5.17)2. x(t) tiene un número finito de máximos y mínimos dentro de cualquier intervalo finito de t.3. x(t) tiene un número finito de discontinuidades dentro de cualquier intervalo finito de t, y cada una de estas discontinuidades es finita.Observe que las condiciones de Dirichlet son suficientes, pero no necesarias para la representación en serie deFourier (problema 5.8).F. ESPECTROS DE AMPLITUD Y DE FASE DE UNA SEÑAL PERIÓDICAExpresemos a los coeficientes complejos de Fourier ck en la ecuación (5.4) de la siguiente manera:ck(5.18)²c k² e jfkA una gráfica de ) ck ) contra la frecuencia angular v se le llama espectro de amplitud de la señal periódica x(t), y a unagráfica de fk contra v se le conoce como espectro de fase de x(t). Puesto que el índice k supone solamente enteros,los espectros de amplitud y de fase no son curvas continuas sino que aparecen sólo como frecuencias discretas kv0.Por tanto, se les conoce como espectro de frecuencias discretas o espectro de líneas.Para una señal periódica real x(t) tenemos que c2k 5 c*k . De este modo,²c k²²ck ²ffkk(5.19)Por tanto, el espectro de amplitud es una función par de v, y el espectro de fase es una función impar de v para unaseñal periódica real.G. CONTENIDO DE POTENCIA DE UNA SEÑAL PERIÓDICAEn el capítulo 1 (problema 1.18) introdujimos la potencia promedio de una señal periódica x(t) sobre un periodo comoP"1T0µT0x (t )2dt(5.20)
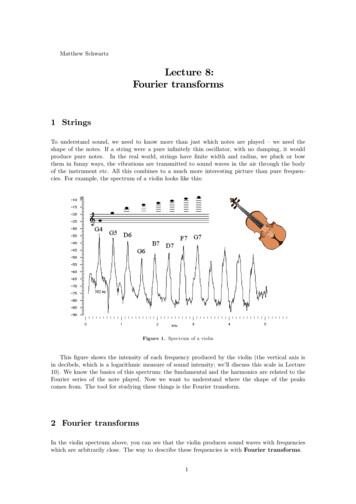
5.3 LA TRANSFORMADA DE FOURIER155Si x(t) está representada mediante la serie de Fourier exponencial compleja en la ecuación (5.4), entonces puededemostrarse que (problema 5.14)h12xtdt()(5.21) ck 2µT0 T0hkLa ecuación (5.21) se conoce como identidad de Parseval (o teorema de Parseval) para la serie de Fourier.5.3LA TRANSFORMADA DE FOURIERA. DE LA SERIE DE FOURIER A LA TRANSFORMADA DE FOURIERSea x(t) una señal no periódica de duración finita; es decir,) t ) . T1x(t) 5 0En la figura 5-1a) se ilustra una señal de este tipo. Sea xT0 (t) una señal periódica formada al repetir x(t) con periodofundamental T0 como se muestra en la figura 5-1b). Si hacemos que T0 S q, tenemos que(5.22)lím xT0 (t ) ! x (t )T0 qhx(t)xT0(t)"T1 0 T1t"T0a)"T0 "T1 0 T1 T02b)T02T0t2Figura 5-1 a) Señal no periódica x(t); b) señal periódica formada porextensión periódica de x(t).La serie de Fourier exponencial compleja de xT0 (t) está dada porhxT0 (t )kdonde jk v 0 t2pT0v0h1T0ckCk eµT0 / 2jk v0 tx (t ) eT0 / 2 T0dt(5.23)(5.24a)Puesto que xT0 (t) 5 x(t) para ) t ) , T0@2 y también x(t) 5 0 fuera de este intervalo, la ecuación (5.24a) puede volvera escribirse como1 T0 / 21 h(5.24b)ckx (t ) e jk v 0 t dtµµ h x(t ) e jk v 0t dtT/20T0T0Definamos X(v) comohµX ( v)hx(t ) ej vtdt(5.25)Entonces, de la ecuación (5.24b), los coeficientes complejos de Fourier ck pueden expresarse comock !1X (k v 0 )T0(5.26)Sustituyendo la ecuación (5.26) en la ecuación (5.23), tenemos quehxT0 (t )k1X ( k v0 ) e jkv0 tTh 0 hoxT0 (t )1 X (k v0 ) e jkv0t v02p k h(5.27)
156CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUOA medida que T0 S q, v0 5 2p@T0 se convierte en infinitesimal (v0 S 0). De este modo, sea v0 5 Dv. Entonces laecuación (5.27) se convierte enh1(5.28)xT0 (t )qX ( k Dv) e jkDvtDv T0 qh2p k hhPor consiguiente,x (t )lím xT0 (t )1 X (k Dv) e jkDvtDv2p k hlímT0 qhDq0(5.29)La suma del lado derecho de la ecuación (5.29) puede visualizarse como el área bajo la función X(v)e jvt, como semuestra en la figura 5-2. Por tanto, obtenemosx (t )12pµhhX ( v)e j v t d v(5.30)lo cual es la representación de Fourier de una señal x(t) no periódica.X(v)e jvtÁrea 5 X(kDv) e jkDvt DvX(kDv)e jkDvtDv0k DvvFigura 5-2 Interpretación gráfica de la ecuación (5.29).B. PAR DE LA TRANSFORMADA DE FOURIERLa función X(v) definida por la ecuación (5.25) se conoce como transformada de Fourier de x(t), mientras que laecuación (5.30) define la transformada de Fourier inversa de X(v). De manera simbólica se denotan medianteX ( v)x (t )!µ! { x (t )}1hhx (t ) e jvt dt1 hX ( v ) e jvt d v2p µ h{ X ( v )}(5.31)(5.32)y decimos que x(t) y X(v) forman un par de transformadas de Fourier denotado porx(t) O X( v)(5.33)C. ESPECTRO DE FOURIERLa transformada de Fourier X(v) de x(t) es, en general, compleja, y puede expresarse comoX( v )²X( v )² e jf(v)(5.34)Por analogía con la terminología utilizada para los coeficientes complejos de Fourier de una señal periódica x(t), latransformada de Fourier X(v) de una señal no periódica x(t) es la especificación en el dominio de la frecuencia de x(t)y se hace referencia a ella como espectro (o espectro de Fourier) de x(t). La cantidad ) X(v) ) se conoce como espectrode magnitud de x(t), mientras que f(v) se denomina espectro de fase de x(t).Si x(t) es una señal real, entonces de la ecuación (5.31) obtenemosX ( v)µhhx (t )e j v t dt(5.35)
5.3 LA TRANSFORMADA DE FOURIEREntonces se deriva queX( v)²X( v)²y(5.36a)X*( v)²X( v)²157f ( v)(5.36b)f (v)Por tanto, como en el caso de las señales periódicas, el espectro de amplitud ) X(v) ) es una función par y el espectrode fase f(v) es una función par de v.D. CONVERGENCIA DE LAS TRANSFORMADAS DE FOURIERDel mismo modo que en el caso de las señales periódicas, las condiciones suficientes para la convergencia de X(v)son las siguientes (de nueva cuenta, se hace referencia a ellas como las condiciones de Dirichlet):1. x(t) es absolutamente integrable; es decir,µhx (t ) dthh(5.37)2. x(t) tiene un número finito de máximos y mínimos dentro de cualquier intervalo finito.3. x(t) tiene un número finito de discontinuidades dentro de cualquier intervalo finito, y cada una de estas discontinuidades es finita.Aunque las condiciones de Dirichlet anteriores garantizan la existencia de la transformada de Fourier para una señal,si se permiten las funciones impulso en la transformada, las señales que no satisfacen estas condiciones pueden tenertransformadas de Fourier (problema 5.23).E. CONEXIÓN ENTRE LA TRANSFORMADA DE FOURIER Y LA TRANSFORMADA DE LAPLACELa ecuación (5.31) define la transformada de Fourier de x(t) comoX ( v)µhx (t ) ehj vt(5.38)dtLa transformada de Laplace bilateral de x(t), como se define en la ecuación (4.3), está dada porµX (s)hhx (t ) est(5.39)dtComparando las ecuaciones (5.38) y (5.39), observamos que la transformada de Fourier es un caso especial de latransformada de Laplace en la cual s 5 jv; esto es,(5.40)X ( s ) s ! j v ! ! { x (t )}Si establecemos s 5 s 1 jv en la ecuación (5.39) tenemos queX (Xoj\ )µhhx (t )eX (s(sj v)j v )tdtµh! { x (t )eh[ x (t )est}st]ejv tdt(5.41)lo que indica que la transformada bilateral de Laplace de x(t) puede interpretarse como la transformada de Fourierde x(t)e2st.Puesto que la transformada de Laplace puede considerarse una generalización de la transformada de Fourier enla cual la frecuencia está generalizada de jv a s 5 s 1 jv, la variable compleja s a menudo se conoce como frecuencia compleja.Observe que puesto que la integral en la ecuación (5.39) está denotada por X(s), la integral en la ecuación (5.38)puede denotarse como X( jv). De este modo, en el resto de este libro tanto X(v) como X( jv) significarán lo mismo siasociamos la transformada de Fourier con la transformada de Laplace. Debido a que la transformada de Fourier esla transformada de Laplace con s 5 jv, no debe suponerse automáticamente que la transformada de Fourier de unaseñal x(t) es la transformada de Laplace con s reemplazada con jv. Si x(t) es absolutamente integrable, es decir, six(t) satisface la condición (5.37), la transformada de Fourier de x(t) puede obtenerse de la transformada de Laplacede x(t) con s 5 jv. Esto no es cierto en general en señales que no son absolutamente integrables. Los siguientesejemplos ilustran los enunciados anteriores.
158CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUOEJEMPLO 5.1Considere la función impulso unitario d(t).De la ecuación (3.13), la transformada de Laplace de d(t) es{ d (t)}(5.42)para toda s1Por las definiciones (5.31) y (1.20), la transformada de Fourier de d(t) esµ! {d(t )}hhjvtd(t )e(5.43)1dtDe este modo, la transformada de Laplace y la transformada de Fourier de d(t) son la misma.EJEMPLO 5.2Considere la señal exponencialx(t)eatu(t)0aDe la ecuación (3.8), la transformada de Laplace de x(t) está dada por" { x (t )}X (s)1sRe ( s )aa(5.44)Por la definición (5.31), la transformada de Fourier de x(t) es! { x (t )}µX ( v)hµ0e(ahhej v )tatu (t ) ejvtdt1dtajv(5.45)De esta forma, al comparar las ecuaciones (5.44) y (5.45) tenemosX( v)X(s)²s(5.46)jvObserve que x(t) es absolutamente integrable.EJEMPLO 5.3Considere la función escalón unitario u(t).De la ecuación (3.14), la transformada de Laplace de u(t) es1Re ( s )sLa transformada de Fourier de u(t) está dada por (problema 5.30)" {u (t )}! {u (t )}pd(v)01jv(5.47)(5.48)De esta manera, la transformada de Fourier de u(t) no puede obtenerse a partir de su transformada de Laplace. Observe que la función escalón unitario u(t) no es absolutamente integrable.5.4PROPIEDADES DE LA TRANSFORMADA DE FOURIERDE TIEMPO CONTINUOLas propiedades básicas de la transformada de Fourier se presentan en la siguiente discusión. Muchas de estas propiedades son semejantes a las correspondientes a la transformada de Laplace (véase la sección 3.4).A. LINEALIDADa1x1(t)B. DESPLAZAMIENTO EN EL TIEMPOa 2 x 2 (t) O a1X1( v )x (t ! t 0 ) O e! j v t0 X ( v)a2 X2 ( v )(5.49)(5.50)La ecuación (5.50) muestra que el efecto de un desplazamiento en el dominio del tiempo sólo implica agregar untérmino lineal 2vt0 al espectro de fase original u(v). Esto se conoce como desplazamiento de fase lineal de la transformada de Fourier X(v).
5.4 PROPIEDADES DE LA TRANSFORMADA DE FOURIER DE TIEMPO CONTINUO159C. DESPLAZAMIENTO EN LA FRECUENCIAe jv 0 t x (t ) O X (v ! v0 )(5.51)En ocasiones, la multiplicación de x(t) por una señal exponencial compleja e jv0t se llama modulación compleja. Deeste modo, la ecuación (5.51) muestra que la modulación compleja en el dominio del tiempo corresponde a un desplazamiento de X(v) en el dominio de la frecuencia. Observe que la propiedad de desplazamiento en la frecuencia[ecuación (5.51)] es la propiedad dual de desplazamiento en el tiempo [ecuación (5.50)].D. ESCALAMIENTO EN EL TIEMPOx (at ) O1 v¹Xª ºa ª« a º»(5.52)donde a es una constante real. Esta propiedad se obtiene directamente de la definición de la transformada de Fourier.La ecuación (5.52) indica que al escalar la variable de tiempo t por el factor a provoca un escalamiento inverso de lavariable de frecuencia v por 1@a, y un escalamiento en amplitud de X(v@a) por 1@) a ). De este modo, la propiedad deescalamiento (5.52) implica que la compresión en el tiempo de una señal (a . 1) produce su expansión espectral, yla expansión en el tiempo de la señal (a , 1) produce su compresión espectral.E. INVERSIÓN DEL TIEMPOx ( t) O X( v)(5.53)De este modo, la inversión del tiempo de x(t) produce una inversión semejante del eje de la frecuencia para X(v). Laecuación (5.53) se obtiene fácilmente al establecer a 5 21 en la ecuación (5.52).F. DUALIDAD (O SIMETRÍA)X(t) O 2p x( v)(5.54)La propiedad de dualidad de la transformada de Fourier tiene implicaciones significativas. Esta propiedad nos permite obtener ambos pares de transformadas de Fourier a partir de una evaluación de la ecuación (5.31) (problemas5.20 y 5.22).G. DIFERENCIACIÓN EN EL DOMINIO DEL TIEMPOdx (t )O j v X ( v)dt(5.55)La ecuación (5.55) muestra que el efecto de la diferenciación en el dominio del tiempo es la multiplicación de X(v)por jv en el dominio de la frecuencia (problema 5.28).H. DIFERENCIACIÓN EN EL DOMINIO DE LA FRECUENCIA(!jt ) x (t ) OdX ( v)dv(5.56)La ecuación (5.56) es la propiedad dual de la ecuación (5.55).I. INTEGRACIÓN EN EL DOMINIO DEL TIEMPOµthx (t ) d t O p X (0 ) d ( v)1X ( v)jv(5.57)
160CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUOPuesto que la integración es la inversa de la diferenciación, la ecuación (5.57) muestra que la operación en el dominio de la frecuencia correspondiente a la integración en el dominio del tiempo es la multiplicación por 1@jv, pero senecesita un término adicional para explicar un posible componente de cd en la salida del integrador. Por consiguiente,a menos que X(0) 5 0, se produce un componente de cd por el integrador (problema 5.33).J. CONVOLUCIÓNx1(t) * x 2 (t) O X1(v) X2(v)(5.58)La ecuación (5.58) se conoce como teorema de convolución del tiempo, y establece que la convolución en el dominio del tiempo se convierte en multiplicación en el dominio de la frecuencia (problema 5.31). Como en el caso dela transformada de Laplace, esta propiedad de convolución juega un papel importante en el estudio de los sistemasLIT de tiempo continuo (sección 5.5) y también forma el fundamento para nuestra discusión de filtros (sección 5.6).K. MULTIPLICACIÓNx1 (t ) x2 (t ) O1X1 ( v) * X2 (v)2p(5.59)La propiedad de multiplicación (5.59) es la propiedad dual de la ecuación (5.58) y se conoce a menudo como teorema de convolución de la frecuencia. De esta forma, la multiplicación en el dominio del tiempo se convierte en laconvolución en el dominio de la frecuencia (problema 5.35).L. PROPIEDADES ADICIONALESSi x(t) es real, seax(t)xe(t)(5.60)xo (t)donde xe(t) y xo(t) son las componentes par e impar de x(t), respectivamente. Seax(t) O X(v)EntoncesA(v)X( v)jB(v)(5.61a)X*(v)xe(t) O Re{X(v)}xo(t) O j Im{X(v)}A( v)(5.61b)jB( v)(5.61c)La ecuación (5.61a) es la condición necesaria y suficiente para que x(t) sea real (problema 5.39). Las ecuaciones(5.61b) y (5.61c) muestran que la transformada de Fourier de una señal par es una función real de v y que la transformada de Fourier de una señal impar es una función imaginaria pura de v.M. RELACIONES DE PARSEVALµhhµx1 (l ) X2 (l ) d lhhµx1 (t ) x2 (t ) dthhx (t )2dtµhhX1 (l ) x2 (l ) d l12pµh12pµhhhX1 (v) X2 ( v) d vX ( v)2dv(5.62)(5.63)(5.64)La ecuación (5.64) se conoce como identidad de Parseval (o teorema de Parseval) para la transformada de Fourier.Observe que la cantidad en el lado izquierdo de la ecuación (5.64) es el contenido de energía normalizada E de x(t)[ecuación (1.14)]. La identidad de Parseval nos dice que este contenido de energía E puede calcularse al integrar) X(v) )2 sobre todas las frecuencias v. Por esta razón, a menudo se conoce a ) X(v) )2 como espectro de densidad deenergía de x(t), y la ecuación (5.64) también se conoce como teorema de la energía.La tabla 5-1 contiene un resumen de las propiedades de la transformada de Fourier que se presentan en estasección. En la tabla 5-2 se proporcionan algunas señales comunes y sus transformadas de Fourier.
5.4 PROPIEDADES DE LA TRANSFORMADA DE FOURIER DE TIEMPO CONTINUOTabla 5-1 Propiedades de la transformada de FourierPropiedadSeñalTransformada de Fourierx(t)X(v)x1(t)X1(v)x2(t)X2(v)a1x1(t) 1 a2 x2(t)a1X1(v) 1 a2X2(v)Desplazamiento en el tiempox(t 2 t0)e2jvt0 X(v)Desplazamiento en la frecuenciae jv0 t x(t)X(v 2 v0)Escalamiento en el tiempox(at)1 v X )a) a Inversión del tiempox(2t)X(2v)X(t)2p x(2v)dx(t)dtjvX(v)Diferenciación en la frecuencia(2jt)x(t)dX( v )dvIntegración Convoluciónx1(t) * x2(t)X1(v)X2(v)x1(t)x2(t)1X1 ( v ) * X2 ( v )2px(t) 5 xe(t) 1 xo(t)X(v) 5 A(v) 1 jB(v)X(2v) 5 X*(v)Componente parxe(t)Re{X(v)} 5 A(v)Componente imparxo(t)j Im{X(v)}5 jB(v)LinealidadDualidadDiferenciación en el tiempot2 MultiplicaciónSeñal realx(t ) dtRelaciones de Parseval x1 ( l )X2 ( l ) dl 5 X1 (l )x2 ( l ) d l 1 x1 (t)x2 (t) dt 5 2p X1 (v )X2 ( v) dv 2) x(t) ) dt 51 2) X( v ) ) dv2p pX(0) d ( v)11X( v )jv161
162CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUOTabla 5-2 Pares comunes de transformadas de FourierX(v)x(t)d (t)1d (t ! t0)1e!jvt02pd(v)e jv 0 t2pd(v ! v0 )cos v0 tp[d (v ! v0 ) # d (v # v0 )]sen v0 t! j p[d (v ! v0 ) ! d (v # v0 )]1pd (v) #jv1pd ( v) !j1jv # a1u(t)u(! t)e!at u(t), a " 0t e!at u(t), a " 0( jv # a)22ae !a t , a " 0a2 # v 212a #te a v 2e!at , a " 0p !v 2 / 4 aea 1 t % apa (t) 0 t " asen v ava 1 v % apa ( v ) 0 v " a2jv22asen atptsgn t d (t ! kT )v0k ! 5.5 d (v ! k v 0 ), v 0 k ! 2pTLA RESPUESTA EN FRECUENCIA DE LOS SISTEMAS LITDE TIEMPO CONTINUOA. RESPUESTA EN FRECUENCIAEn la sección 2.2 demostramos que la salida y(t) de un sistema LIT de tiempo continuo es igual a la convolución dela entrada x(t) con la respuesta al impulso h(t); es decir,y(t)x(t) * h(t)(5.65)Al aplicar la propiedad de convolución (5.58) obtenemosY(v )X(v)H(v)(5.66)donde Y(v), X(v) y H(v) son las transformadas de Fourier de y(t), x(t) y h(t), respectivamente. De la ecuación (5.66)tenemos que
5.5 LA RESPUESTA EN FRECUENCIA DE LOS SISTEMAS LIT DE TIEMPO CONTINUOH (v ) !Y ( v)X ( v)(5.67)La función H(v) se conoce como respuesta en frecuencia del sistema.Las relaciones representadas mediante las ecuaciones (5.65) y (5.66) seilustran en la figura 5-3. SeaH(v)(5.68)²H( v)²e j uH (v)Entonces ) H(v) ) se denomina respuesta de magnitud del sistema, yuH(v) respuesta de fase del sistema.Considere la señal exponencial compleja1d(t)x(t)X(v)H(v)SistemaLITh(t)y(t)5x(t) * h(t)Y(v)5X(v)H(v)Figura 5-3 Relaciones entre entradas ysalidas en un sistema LIT.(5.69)e j v 0tx(t)163con transformada de Fourier (problema 5.23)X(v)2 pd ( vv0 )(5.70)Entonces, de las ecuaciones (5.66) y (1.26) tenemos que2pH( v0 ) d ( vY( v)v0 )(5.71)Al tomar la transformada de Fourier inversa de Y(v) obtenemos(5.72)H( v0 ) e j v 0ty(t )jv0tlo cual indica que la señal exponencial compleja e es una función propia del sistema LIT con un valor propiocorrespondiente H(v0), como se observó previamente en el capítulo 2 (sección 2.4 y problema 2.17). Además, por lapropiedad de linealidad (5.49), si la entrada x(t) es periódica con la serie de Fourierhx (t )k ck e jk v0t(5.73)hentonces la salida y(t) correspondiente también es periódica con la serie de Fourierhy(t )k ck H ( k v 0 ) e jkv0 t(5.74)hSi x(t) no es periódica, entonces de la ecuación (5.30)x (t )12pµhhX ( v ) e j vt d v(5.75)y mediante la ecuación (5.66), la salida correspondiente y(t) puede expresarse comoy(t )12pµhhH ( v ) X ( v ) e j vt d v(5.76)De este modo, el comportamiento de un sistema LIT de tiempo continuo en el dominio de la frecuencia está completamente caracterizado por su respuesta en frecuencia H(v). SeaX( v)²X( v)²e j uX (v)Y( v)²Y( v)²e j uY (v)(5.77)Entonces, de la ecuación (5.66) tenemos que²Y( v)²uY (v )²X( v)²²H(v)²(5.78a)uX ( v)(5.78b)uH ( v)Por consiguiente, el espectro de magnitud ) X(v) ) de la entrada se multiplica por la respuesta de magnitud ) H(v) ) delsistema para determinar el espectro de magnitud ) Y(v) ) de la salida, y la respuesta de fase uH(v) se suma al espectrode fase uX (v) de la entrada para producir el espectro de fase uY (v) de la salida. La respuesta de magnitud ) H(v) ) seconoce a menudo como ganancia del sistema.
164CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUOB. TRANSMISIÓN SIN DISTORSIÓNPara transmitir sin distorsión a través de un sistema LIT necesitamos que la forma exacta de la señal de entrada sereproduzca en la salida, aunque su amplitud puede ser diferente y estar atrasada en el tiempo. Por tanto, si x(t) es laseñal de entrada, la salida necesaria esy(t) Kx(t td )(5.79)donde td es el atraso en el tiempo (time delay) y K (. 0) es una constante de ganancia. Esto se ilustra en la figura5-4a) y b). Tomando la transformada de Fourier de ambos lados de la ecuación (5.79) obtenemosY( v)Kej v td(5.80)X( v)De esta forma, de la ecuación (5.66) observamos que para una transmisión sin distorsión el sistema debe tener²H( v)²e j uH(v)H( v)²H( v)²De este modo,Ke(5.81)j v td(5.82a)KuH (v)(5.82b)jvtdEs decir, la amplitud de H(v) debe ser constante sobre todo el intervalo de frecuencias, mientras que la fase de H(v)debe ser lineal con la frecuencia. Esto se ilustra en la figura 5-4c) y d).) H(v) )x(t)AK0tt1v0a)c)y(t)uH(v)KA0tdt11 td0td)b)vDeclive 5 2tdFigura 5-4 Transmisión sin distorsión.DISTORSIÓN DE AMPLITUD Y DISTORSIÓN DE FASECuando el espectro de amplitud ) H(v) ) del sistema no es constante dentro de la banda de frecuencia de interés, loscomponentes de frecuencia de la señal de entrada se transmiten con una cantidad diferente de ganancia o atenuación.Este efecto se denomina distorsión de amplitud. Cuando el espectro de fase uH(v) del sistema no es lineal con lafrecuencia, la señal de salida tiene una forma de onda diferente de la señal de entrada debido a los diferentes retardos al pasar a través del sistema por los diferentes componentes de frecuencia de la señal de entrada. Esta forma dedistorsión se denomina distorsión de fase.C. SISTEMAS LIT CARACTERIZADOS POR ECUACIONES DIFERENCIALESComo se discutió en la sección 2.5, muchos sistemas LIT de tiempo continuo de interés práctico se describen mediante ecuaciones diferenciales lineales con coeficientes constantes de la formaN akk !0Md k y(t )d k x (t )! bkkdtdt kk !0(5.83)
5.6 FILTRADO165con M # N. Cuando tomamos la transformada de Fourier de ambos lados de la ecuación (5.83) y por medio de lapropiedad de linealidad (5.49) y la propiedad de diferenciación en el tiempo (5.55), tenemos queNMk !0k !0Y (v ) ak ( j v)k ! X (v) bk ( jv)k ak ( j v)k Y (v) ! bk ( jv)k X (v)oNMk !0k !0(5.84)De este modo, de la ecuación (5.67)M bk ( j v)kH (v) !Y (v ) k ! 0! NX (v)(5.85) ak ( j v ) kk !0que es una función racional de v. El resultado (5.85) es el mismo que el de la contraparte de la transformada de Laplace H(s) 5 Y(s)@X(s) con s 5 jv [ecuación (3.40)]; es decir,H(v)5.6H(s)²sjvH( j v)FILTRADOUna de las operaciones fundamentales en cualquier sistema de procesamiento de señales es el filtrado; éste es elproceso mediante el cual las amplitudes relativas de los componentes de frecuencia en una señal se modifican oquizá algunos componentes de frecuencia se suprimen. Como vimos en la sección precedente, para los sistemas LITde tiempo continuo el espectro de la salida es igual al de la entrada multiplicado por la respuesta en frecuencia delsistema. Por tanto, un sistema LIT actúa como filtro sobre la señal de entrada. Aquí la palabra “filtro” se utiliza paradenotar un sistema que exhibe alguna clase de comportamiento selectivo de frecuencias.A. FILTROS IDEALES DE FRECUENCIA SELECTIVAUn filtro ideal de frecuencia selectiva es aquel que permite el paso exacto de señales en un determinado intervalo defrecuencias y rechaza completamente el resto. La banda de frecuencias que pasa por el filtro se conoce como bandade paso o pasa-banda, mientras que la banda de frecuencias rechazadas por el filtro se denomina banda de rechazoo supresora de banda.Los tipos más comunes de filtros de frecuencia selectiva son los siguientes:1. FILTRO IDEAL PASA-BAJASUn filtro ideal pasa-bajas (LPF, low-pass filter) está especificado porH (v ) ²1 ²0vvcvvc(5.86)el cual se muestra en la figura 5-5a). La frecuencia vc se conoce como frecuencia de corte.2. FILTRO IDEAL PASA-ALTASUn filtro ideal pasa-altas (HPF, high-pass filter) está especificado porH ( v)el cual se muestra en la figura 5-5b).² 0 ²1vvvcvc(5.87)
166CAPÍTULO 5 ANÁLISIS DE FOURIER DE SEÑALES Y SISTEMAS DE TIEMPO CONTINUO3. FILTRO IDEAL PASA-BANDAUn filtro ideal pasa-banda (BPF, bandpass filter) está especificado por 1 0H (v )v1v v2de otro modo(5.88)el cual se muestra en la figura 5-5c).4. FILTRO IDEAL SUPRESOR DE BANDAUn filtro ideal supresor de banda (BSF, bandstop filter) está especificado por 0 1H ( v)v1vv2(5.89)de otro modoel cual se muestra en la figura 5-5d).) H(v) )) H(v) )12vc01vcv2vca)0vcb)) H(v) )) H(v) )112v2 2v10vv1v22v2 2v1v0v1v2vd)c)Figura 5-5 Respuestas de magnitud de filtros ideales de frecuencia selectiva.En la discusión anterior no mencionamos nada sobre la respuesta de fase de los filtros. Para evitar la distorsiónde fase en el proceso de filtrado, un filtro debe tener una característica de fase lineal sobre la banda de paso del filtro;esto es [ecuación (5.82b)],uH (v)vtd(5.90)donde td es una constante.Observe que todos los filtros ideales de frecuencia selectiva son sistemas no causales.B. FILTROS NO IDEALES DE FRECUENCIA SELECTIVAConsideraremos el filtro RC mostrado en la figura 5-6a) como un ejemplo de un filtro simple de frecuencia selectivacausal de tiempo continuo. La salida y(t) y la entrada x(t) están relacionadas mediante (problema 1.32)RCdy(t )dty(t )x (t )Tomando las transformadas de Fourier de ambos lados de la ecuación anterior, la respuesta en frecuencia H(v) delfiltro RC está dada por11Y (v )(5.91)H (v)X ( v) 1 j vRC 1 j v /v 0
5.7 ANCHO DE BANDAdonde v0 5 1@RC. De esta manera, la respuesta de amplitud ) H(v) ) y larespuesta de fase uH(v) están dadas porH (\ )1j\ / \ 01V H (\ )1 1 tan1R11(5.92)1/ 2(\ / \ 0 )2 ¼¾167i(t)x(t)C22\\0y(t)(5.93)a)) H(v) )lo que se grafica en la figura 5-6b). De la figura 5-6b) observamos que lared RC en la figura 5-6a) actúa como un filtro pasa-bajas.15.7 ANCHO DE BANDA1/ 2A. ANCHO DE BANDA DEL FILTRO (O SISTEMA)2v0Un concepto importante en el análisis de sistemas es el ancho d
CAPÍTULO 5 Análisis de Fourier de señales y sistemas de tiempo continuo 5.1 INTRODUCCIÓN En capítulos anteriores presentamos la transformada de Laplace y la transformada z para convertir las señales en el dominio del tiempo en representaciones en el dominio s y el dominio z complejos que son, para muchos propósitos, más convenientes para analizar y procesar.