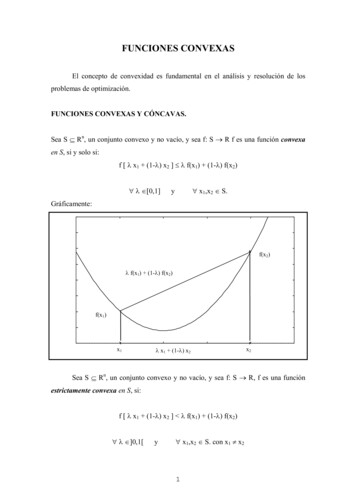
Transcription
Función Definición:– Sean A y B conjuntos no vacíos. Una función de A en B es una relaciónque asigna a cada elemento x del conjunto A uno y solo un elementoy del conjunto B.Se expresa como:f: AxBf(x) ySe dice que y es la imagen de x mediante f, y que x es lapre-imagen de f(x) y
Función Conceptos:– Dominio: es el conjunto de todos los valores para los cualesestá definida la función y se denota Dom f.– Recorrido: es el conjunto de todos los valores que toma lavariable independiente (Y), y se denota Rec f.– Función Creciente: es aquella que al aumentar la variableindependiente, también aumenta la variabledependiente.– Función Decreciente: es aquella que al aumentar la variableindependiente, la variable dependiente disminuye.– Función Constante: es aquella que para todos los valores de lavariable independiente, la variable dependientetoma un único valor
Función Función Continua:Es aquella en la que su gráfica se puede recorrer en formaininterrumpida en toda su extensión.
Función Función Discontinua:Es aquella que no es continua, es decir, presenta separaciones y/osaltos en su gráfica.
Función Función Periódica:Es aquella en la que su gráfica se repite cada cierto intervalo, llamadoperíodo.
Función Conceptos Fundamentales:– Si tenemos una relación f entre dos conjuntos A y B, f se dirá funciónsi a cada valor del conjunto de partida A le corresponde uno y sólo unvalor en el conjunto de llegada B.AfBab f(a)xf(x)f(x)
Función Conceptos Fundamentales:– La variable x corresponde a la variable independiente y la variablecuyo valor viene determinado por el que toma x, se llama variableindependiente. Se designa generalmente por y o f(x) [se lee “f de x”].Decir que “y” es función de “x” equivale a decir que “y” depende de“x”.fABab f(a)xf(x)
Funcióno Conceptos FundamentalesSe dirá:– f:AB– b B es la imagen de a A bajo la función f y se denota por– Dom f A– Si (x, y) f (x, z) fy z (Unívoca)Toda función es relación, pero no toda relaciónes función.b f(a)
Función– Rango o Recorrido de f:Es aquel subconjunto del codominio en el cual todos sus elementosson imagen de alguna preimagen del dominio o conjunto de partida.Se denota por Rec f.fAB1a2b3c4d5e67Se puede ver que para todo elemento de A, existe sólo unaimagen en B.
Luego para la función f denotada:AabcdefB1234567– Dominio de f Dom f A {a, b, c, d, e}– Codominio B {1, 2, 3, 4, 5, 6, 7}– Rango o Recorrido de f Rec f {1, 2, 3, 4, 7}Los elementos {5, 6} no son imagen de ningunapreimagen en A, luego no pertenecen al rango de f .
Clasificación a) Función Inyectiva: Una inyección de A en B es toda f de A en B, demodo que a elementos distintos del dominio A le corresponden imágenesdistintas en el codominio B.Cada elemento de A tiene una única imagen en B (y sólo una), de tal formaque se verifica que # A # B.fAabcd12345BComo se ve, 4 B y no es imagen de ningún elemento de A
b) Función Epiyectiva o Sobreyectiva: Una epiyección o sobreyección de Aen B, de modo que todo elemento del codominio B es imagen de, al meno,un elemento del dominio A. Cada elemento de B es imagen de por lomenos un elemento de A. Se verifica que # A # B. Es decir, que en estecaso el codominio es igual al recorrido.fAabcdB12
c) Función Biyectiva: una función f es biyectiva de A en B si y sólo si lafunción f es tanto Inyectiva como Epiyectiva a la vez, por lo que se verificaque #A #B y que a cada elemento de A le corresponde una única imagenen B y que cada imagen de B le corresponde una preimagen en A.fAabcB123
FunciónLa Respuesta correcta es B
FunciónLa Respuesta correcta es D
FunciónLa Respuesta correcta es E
I. Función Lineal Es de la forma f(x) mx ncon m : Pendienten : Ordenada del punto de intersección entre la recta y el(coeficiente de posición).Ejemplo:La función f(x) 5x – 3, tiene pendiente 5 e intersecta al eje Y en laordenada -3.eje Y
I. Función Lineal Análisis de la PendientePara saber con qué tipo de función se está trabajando, se debe analizar elsigno de la pendiente. Si m 0, entonces la función es decreciente. Si m 0, entonces la función es constante. Si m 0, entonces la función es creciente.
I. Función LinealYI)Ym 0n 0nnII)m 0n 0XXYYm 0n 0III)m 0n 0IV)XnXn
I. Función Lineal Tipos de funciones especiales:– a) La función de forma f(x) x, se reconoce como función identidad ysu gráfica es:f(x)21-1-112x
I. Función Lineal Tipos de funciones especiales: b) La función de la forma f(x) c, con c: Constante Real, se conocecomo función constante y su gráfica es:f(x)f(x)con c 0ccon c 0 xxc
I. Función lineal Propiedades:– El dominio de la función lineal son todos los números IR.– Las rectas que tienen la misma m serán paralelas.– Las rectas que al multiplicar sus pendientes el producto es -1 seránperpendiculares.
I. Función Lineal Evaluación de una función lineal:Dada la función f(x) mx n, si se busca el valor de la función para unvalor cualquiera de x, basta reemplazar dicho valor, así como también si sebusca el valor de x conociendo el valor de la función.EjemploLa función que representa el valor a pagar en un taxi, después de recorridos 200mes:f(x) 0.8x 250conx: cantidad de metros recorridosf(x): costo en pesos3 km 3000 mEntonces, el valor a pagar por un recorrido de 3 kilómetros es:f(3000) 0.8 · 3000 250 2650Por 3 kilómetros se pagan 2650.
I. Función LinealSi queremos saber cuántos metros recorrió una persona si pagó 2.250, sedebe resolver la siguiente ecuación:2250 0.8x 2502000 0.8x2500 x/ -250/ :0.8Una persona que paga 2250. recorrió 2500 metros o 2.5 kilómetros.
I. Función Lineal Construcción de una Función Lineal conocidos valores de ella:– Para construir una función lineal se deben conocer dos relacionesdistintas entre el valor de la variable y el valor de la función, es decir:(x , f(x )) y (x , f(x ))O bien si a f(x) le llamamos y, entonces los pares quedan:(x , y ) y (x , y )1122Donde la función buscada será:1122y – y 11 y22 - y1 1 (x – x 1 )x2 - x1211
I. Función Lineal EjemploSi se sabe que el agua se congela a 32º F ó 0º C y hierve a 212º F ó100º C, ¿cómo se puede expresar los ºF como función lineal de los ºC?Solución:Se tiene la siguiente información:xy y1(0, 32)1x2y2(100, 212)Cº : variable independiente (x)ºF : variable dependiente (y)
I. Función LinealReemplazando en:Se tiene:y – y 1 y 2 - y 1 (x – x )1x 2 - x1y – 32 212 – 32 (x – 0)100 – 0y – 32 180 . x100y 1.8· x 32Donde la función que representa los ºF respecto de ºC es.f(x) 1.8· x 32
I. Función LinealSe le llama crecimiento aritmético a la progresión cuyos términosaumentan en una misma cantidad constante llamada diferencia. Estecrecimiento aritméticográficamente está representado por una rectacon pendiente positiva. Si la pendiente es negativa se habla de undecrecimiento aritmético.Ejemplo:f (x) 2x 1f (0) 2· 0 1 1f (1) 2· 1 1 3 2f (2) 2· 2 1 5 2f (3) 2· 3 1 7 2
I. Función Lineal Gráficamente53112
II. Función Cuadrática Son de la forma:f(x) ax² bx c Gráfica:Siempre es una parábola, dependiendo su forma yla ubicación de sus coeficientes a, b y c.
II. Función Cuadrática Concavidad:El coeficiente a de la función cuadrática indica si la parábola es abiertahacia arriba o hacia abajo.yy00xxa 0, Abierta hacia arribaa 0, Abierta hacia abajo
II. Función Cuadrática Eje de simetría y vértice:El eje de simetría es aquella recta paralela al eje Y y que pasa por elvértice de la parábola.El vértice está dado por:Vértice -b , f -b2a2a -b , 4ac – b²2a4a
II. Función CuadráticaAdemás, la recta x -b, corresponde al Eje de simetría.2ayyb² - 4ac4aa 0-b2ab² - 4ac4a·x0-b2a·a 0x
II. Función Cuadrática Intersección con los ejes– Intersección con el eje YEl coeficiente c nos da el punto en el cual la parábola corta al eje Y.Sus coordenadas son (0, c)yc·0x
II. Función Cuadrática– Intersección con el eje Xpara determinar el o los puntos donde la parábola corta al eje X, esnecesario conocer el valor del discriminante de la función cuadrática.Se define el discriminante como:D b² - 4ac
II. Función Cuadrática a) Si el D 0, la parábola corta en un solo punto al eje X.Ya 0(x x , 0)120·X
II. Función Cuadrática b) Si el D 0, la parábola corta en dos puntos al eje XYa 0(x ,0) y (x , 0)120··X
II. Función Cuadrática c) Si el D 0, la parábola no corta al eje X.Y0a 0X
II. Función Cuadrática a) Si el D 0, la parábola corta en un solo punto al eje X.Ya 0(x x , 0)120·X
II. Función Cuadrática b) Si el D 0, la parábola corta en dos puntos al eje XYa 0(x ,0) y (x , 0)120··X
II. Función Cuadrática c) Si el D 0, la parábola no corta al eje X.Y0a 0X
II. Función Cuadrática Naturaleza de las raíces de una ecuación de 2º gradoSi f(x) 0, tendremos que ax² bx c 0, llamada Ecuación de 2º gradoen su forma general.Toda ecuación de 2º grado posee dos soluciones, pudiendo ser reales oimaginarias, las que vienen dadas por la expresión:x -b b²- 4ac2a1x -b b²- 4ac2a2x -b b²- 4ac2aEstas soluciones, raíces o ceros de la ecuacióncorresponden gráficamente a los puntos donde la funciónf(x) ax² bx c corta al eje X. Estos puntos tienen comocoordenadas (x 1 ,0) y (x2 , 0)
II. Función Cuadrática Tipos de solucionesD b² - 4acDependen del valor del Discriminante(x1 y)1a) Si D 0, 2 soluciones reales iguales1122b) Si D 0, 2 soluciones reales distintas (x y x C, con x x )121c) Si D 0, 2 soluciones imaginarias distintas (x y x C, con x x )2
II. Función Cuadrática Ejemplo:– Sea la ecuación de 2º grado: x² 2x – 15 0. ¿Cuáles son las soluciones de estaecuación?Sabemos que las soluciones de una ecuación de 2º grado vienen dadas porx -b b²- 4ac2aa 1b 2c -15En este casoLuego,Luego,x -2 2²- 4·1·(-15)2·1x -2 4- 602x -2 642x -2 82x -2 81x -2 - 8222x 3x -512
III. Función Parte Entera Su valor, para cada número x IR, es la parte entera de x y se designa por[x]. Ésta se escribe:f(x) [x] Dado un número real x, la función parte entera le asigna el mayor enteroque es menor o igual a x, es decir:[x] x [x 1]Ejemplos:[2,9] 2;[-7/2] -4;[5] 5;[ 2] 1Todo número real está comprendido entre dos númerosenteros, la parte entera de un número es el menor delos números enteros entre los que está comprendido.
III. Función Parte EnteraObsérvese que esta función es constante en los intervalossemiabiertos (semicerrados) de la forma [n, n 1[ con n Z.Por tanto, los segmentos horizontales contienen susextremos izquierdos, pero no los derechos
IV. Función Valor Absoluto El valor absoluto de un número x IR, denotado por x , es siempre unnúmero real no negativo que se define:x si x 0f(x) x -x si x 0Ejemplo: -3 3 12 12 -18 18 -5,3 5,3Si los números reales están representadosgeométricamente en el eje real, el número x sellama distancia de x al origen.
IV. Función Valor Absoluto– a indica el punto de traslación en el eje de las coordenadas.
IV. Función Valor Absoluto– b indica el punto de traslación en el eje de las abscisas.
IV. Función Valor Absoluto Propiedades:– a. Si x a entonces -a x a; con a 0– b. Si x a entonces x a ó -x a– c. xy x · y – d. x y x y (Desigualdad Triangular)
IV. Función Valor Absoluto Propiedades:– a. Si x a entonces -a x a; con a 0– b. Si x a entonces x a ó -x a– c. xy x · y – d. x y x y (Desigualdad Triangular)
IV. Función Valor Absoluto La última propiedad se llama desigualdad triangular, pues, cuando, segeneraliza a vectores indica que la longitud de cada lado de un trianguloes menor o igual a la suma de las longitudes de los otros dos.
IV. Función Valor Absoluto Ejercicios:– Determinar el intervalo solución de las siguiente inecuación: a. x – 3 2Aplicando la primera propiedad:-2 x – 3 2-2 3 x 2 31 x 5x [1, 5]
IV. Función Valor AbsolutoLa Respuesta correcta es B
IV. Función Valor AbsolutoLa Respuesta correcta es D
V. Función Exponencial Es la función inversa del logaritmo natural y se denota equivalentementecomo: xe x o xexp(x)La función exponencial f con base a se define comof(x) axSi a 0 a 1, x IR
V. Función Exponencial Propiedades:– El dominio de la función exponencial está dado por los números IR.– El recorrido de la función exponencial está dado por los IR*.– El punto de intersección de la función con el eje Y es (0, 1).– La función no intercepta el eje X.
V. Función Exponencial Crecimiento y decrecimiento exponencial:– Si 0 a 1, f(x) es decreciente en IR
V. Función Exponencial Ejercicio:– Determinar la función que representa en número de bacterias que hay en unapoblación después de x horas si se sabe que inicialmente había 10.000 bacterias yque la población se triplica cada una hora.Solución:Cantidad inicial 10.000Después de una hora 10.000 · 3 30.000Después de dos horas 10.000 · 3 · 3 90.000x Después de x horas 10.000· 3Por lo tanto, siendo x el número de horas que pasan desde el inicio del estudio, lacantidad de bacterias se representa por la función:f(x) 10.000 · 3x
V. Función Logarítmica La inversa de una función exponencial de base a se llama funciónlogarítmica de base a y se representa por loga.– Está dada por la siguiente ecuación:y loga xsix ay
V. Función Logarítmica Propiedades– El dominio de la función logarítmica está dado por los números IR, lafunción no está definida para x 0.– El punto de intersección de la función con el eje X es (1, 0).– La función no intercepta el eje Y.
V. Función Logarítmica Crecimiento y decrecimiento Logarítmico:– Si a 1, f(x) log xaes creciente para x 0.
V. Función Logarítmica Crecimiento y decrecimiento Logarítmico:– Si 0 a 1, f(x) log x es decreciente para x 0.a
V. Función Logarítmica Ejercicios:– Dado los valores: log 2 0.3010 y log 3 0.4771. Entonces, en la función f(x) log x,determine f(6).Solución:f(6) log (6)Dondelog 6 log (2 · 3)Por Propiedadlog (2 · 3) log 2 log 3 0.3010 0.4771 0.7781Por lo tanto:Si f(x) log x, entonces f(6) 0.7781
V. Función LogarítmicaLa Respuesta correcta es D
Función inversaf 1
EjemploHallar la inversa y grafica de la siguiente funciónf x 2x 1SoluciónPara hallar la inversa de la función debemos despejar la variabley 2x 1y 1 2xy 1 x2Por lo tantof 1x 1 x 2x
EjemploHallar la inversa y grafica de la siguiente funciónf x 2x 1SoluciónPara hallar la inversa de la función debemos despejar la variabley 2x 1y 1 2xy 1 x2Por lo tantof 1x 1 x 2x
Paridad de una funciónFunciones paresDecimos que una función es par siempre que para todo valor de lavariable independiente perteneciente al dominio se cumpla que:f x f x
EjemploDada la funciónf x 3x 2 4 x 4a) ¿es par o impar?.SoluciónAnalizaremos si la función es par, para ello debe cumplir quePara este casof x 3 x 4 x 2 3x 2 4 x 4 f x Por lo tanto esta función es par4f x f x
Función ImparDecimos que una función es impar siempre quepara todo valor de la variable independienteperteneciente al dominio se cumpla que:f x f x Función sin paridadEl carácter par o impar de una función es lo queconocemos como su paridad. Las funciones queno son ni pares, ni impares, carecen de paridad.
EjemploDada la funcióna)1g x x x23¿es par o impar?.SoluciónAnalizaremos si la función es impar, para ello debe cumplir quePara este caso13g x x x 21 x3 x2 3 1 x x 2 g x Por lo tanto esta función es imparf x f x
Operaciones con funcionesA C y g: B DDom f Dom g Sean f :dos funciones tal queSuma de f y g f g x f x g x Resta de f y g fProducto de f y g f g x f x g x Cociente de f y gf x f x g x g g x f x g x g x 0
Función CompuestaSeanf : A C y g : B D funciones tales que f A B ,Entonces se llama función compuesta de g y f y lo denotamos porA la función definida por g f x g f x para cada valor de A,tal que su imagen este en el conjunto BGráficamente podemos expresar la función compuesta de g y f dela siguiente manera
Composición de de f y g g f x g f x
Composición de una Función con su InversaDe la representación anterior se puede notar que: f f x x 1o 1f f x x
EjemploConsidere las siguientes funciones reales definidas porg x x2 1f x 5 3xDetermine g f x 1SoluciónPor hallar la inversa def x 5 3xPara este caso la función es biyectiva por lo tanto existe su inversa, la cual esy 5 3x5 yx 3
f 15 x x 3En donde su Dominio es los números realesAdemás el dominio d la funciónPor lo tantoPor lo tantog x También son los números realesDom g f 1 IR 1 1g fx gf x 5 x 5 x g 1 3 3 2Por lo tanto 5 x 1g fx 1 3 2
Función LinealFunción CuadráticasFunción PotenciaFunción RaízFunción CúbicaFunción Reciproca
Función Valor AbsolutoFunción ExponencialesFunción LogarítmicasFunciones Trigonométricasf x Sen x f x Cos x f x Tang x
Funciones Hiperbólicasf x Senh x f x Cosh x f x Tangh x
a) Función Inyectiva: Una inyección de A en B es toda f de A en B, de modo que a elementos distintos del dominio A le corresponden imágenes distintas en el codominio B. Cada elemento de A tiene una única imagen en B (y sólo una), de tal forma que se verifica que # A # B. Como se ve, 4 B y no es imagen de ningún elemento de A a .