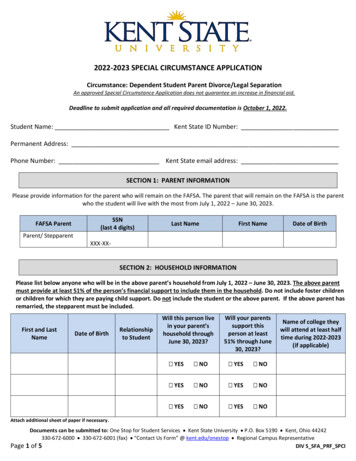
Transcription
00 000200010271308615 CH00 FM pi-viii05/28/201216:20 PMPage 1aPenstioluSoeng alni sar ReLe or r ionftOuon trs NoribDavid C. Lay R. Kent Nagle Edward B. SaffArthur David SniderLinear Algebra &Differential EquationsDSecond Custom Edition for University of California, BerkeleytisTaken from:Linear Algebra and Its Applications, Fourth Editionby David C. LayFundamentals of Differential Equations, Eighth Editionby R. Kent Nagle, Edward B. Saff and Arthur David Snider
00 000200010271308615 CH00 FM pi-viii05/28/201216:20 PMPage 8aPenstioluSoeng alni sar ReLe r r ionoftOuon trs NoribtisD
01 000200010271308615 CH01 p001-09215:00 PMPage 3Linear Equations inLinear AlgebraaPe105/26/2012nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribINTRODUCTORY EXAMPLELinear Models in Economicsand EngineeringtisDIt was late summer in 1949. Harvard Professor WassilyLeontief was carefully feeding the last of his punchedcards into the university’s Mark II computer. The cardscontained economic information about the U.S. economyand represented a summary of more than 250,000 piecesof information produced by the U.S. Bureau of LaborStatistics after two years of intensive work. Leontief haddivided the U.S. economy into 500 “sectors,” such as thecoal industry, the automotive industry, communications,and so on. For each sector, he had written a linear equationthat described how the sector distributed its output tothe other sectors of the economy. Because the Mark II,one of the largest computers of its day, could not handlethe resulting system of 500 equations in 500 unknowns,Leontief had distilled the problem into a system of 42equations in 42 unknowns.Programming the Mark II computer for Leontief’s 42equations had required several months of effort, and hewas anxious to see how long the computer would taketo solve the problem. The Mark II hummed and blinkedfor 56 hours before finally producing a solution. We willdiscuss the nature of this solution in Section 1.6.Leontief, who was awarded the 1973 Nobel Prizein Economic Science, opened the door to a new erain mathematical modeling in economics. His effortsat Harvard in 1949 marked one of the first significantuses of computers to analyze what was then a largescale mathematical model. Since that time, researchersin many other fields have employed computers to analyzemathematical models. Because of the massive amounts ofdata involved, the models are usually linear; that is, theyare described by systems of linear equations.The importance of linear algebra for applications hasrisen in direct proportion to the increase in computingpower, with each new generation of hardware andsoftware triggering a demand for even greater capabilities.Computer science is thus intricately linked with linearalgebra through the explosive growth of parallel processingand large-scale computations.Scientists and engineers now work on problems farmore complex than even dreamed possible a few decadesago. Today, linear algebra has more potential value forstudents in many scientific and business fields than anyother undergraduate mathematics subject! The material inthis text provides the foundation for further work in manyinteresting areas. Here are a few possibilities; others willbe described later. Oil exploration. When a ship searches for offshoreoil deposits, its computers solve thousands ofseparate systems of linear equations every day. The3
01 000200010271308615 CH01 p001-092405/26/201215:00 PMPage 4Linear Algebra and Differential Equations aPeseismic data for the equations are obtained fromunderwater shock waves created by explosionsfrom air guns. The waves bounce off subsurfacerocks and are measured by geophones attached tomile-long cables behind the ship.employs linear programs that schedule flight crews,monitor the locations of aircraft, or plan the variedschedules of support services such as maintenanceand terminal operations. Electrical networks. Engineers use simulationsoftware to design electrical circuits and microchipsinvolving millions of transistors. Such softwarerelies on linear algebra techniques and systems oflinear equations.nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribLinear programming. Many important managementdecisions today are made on the basis of linearprogramming models that utilize hundreds ofvariables. The airline industry, for instance,WEBtisDSystems of linear equations lie at the heart of linear algebra, and this chapter uses them tointroduce some of the central concepts of linear algebra in a simple and concrete setting.Sections 1.1 and 1.2 present a systematic method for solving systems of linear equations.This algorithm will be used for computations throughout the text. Sections 1.3 and1.4 show how a system of linear equations is equivalent to a vector equation and to amatrix equation. This equivalence will reduce problems involving linear combinationsof vectors to questions about systems of linear equations. The fundamental concepts ofspanning, linear independence, and linear transformations, studied in the second half ofthe chapter, will play an essential role throughout the text as we explore the beauty andpower of linear algebra.1.1 SYSTEMS OF LINEAR EQUATIONSA linear equation in the variables x1 ; : : : ; xn is an equation that can be written in theforma1 x1 C a2 x2 C C an xn D b(1)where b and the coefficients a1 ; : : : ; an are real or complex numbers, usually knownin advance. The subscript n may be any positive integer. In textbook examples andexercises, n is normally between 2 and 5. In real-life problems, n might be 50 or 5000,or even larger.The equationsp 4x1 5x2 C 2 D x1 and x2 D 2 6 x1 C x3are both linear because they can be rearranged algebraically as in equation (1):p3x1 5x2 D 2 and 2x1 C x2 x3 D 2 6The equations4x15x2 D x1 x2pand x2 D 2 x16pare not linear because of the presence of x1 x2 in the first equation and x1 in the second.A system of linear equations (or a linear system) is a collection of one or morelinear equations involving the same variables—say, x1 ; : : : ; xn . An example is2x1x1x2 C 1:5x3 D4x3 D87(2)
01 000200010271308615 CH01 p001-09205/26/201215:00 PMCHAPTER 1Page 5Linear Equations in Linear Algebra5aPeA solution of the system is a list .s1 ; s2 ; : : : ; sn / of numbers that makes each equation atrue statement when the values s1 ; : : : ; sn are substituted for x1 ; : : : ; xn , respectively. Forinstance, .5; 6:5; 3/ is a solution of system (2) because, when these values are substitutedin (2) for x1 ; x2 ; x3 , respectively, the equations simplify to 8 D 8 and 7 D 7.The set of all possible solutions is called the solution set of the linear system. Twolinear systems are called equivalent if they have the same solution set. That is, eachsolution of the first system is a solution of the second system, and each solution of thesecond system is a solution of the first.Finding the solution set of a system of two linear equations in two variables is easybecause it amounts to finding the intersection of two lines. A typical problem isnstioluSoeng alni sar ReLe r r ionoftOuon trs Noribx1 2x2 Dx1 C 3x2 D13The graphs of these equations are lines, which we denote by 1 and 2 . A pair of numbers.x1 ; x2 / satisfies both equations in the system if and only if the point .x1 ; x2 / lies on both 1 and 2 . In the system above, the solution is the single point .3; 2/, as you can easilyverify. See Fig. 1.x22Dl23x1tisl1FIGURE 1 Exactly one solution.Of course, two lines need not intersect in a single point—they could be parallel, orthey could coincide and hence “intersect” at every point on the line. Figure 2 shows thegraphs that correspond to the following systems:x1 2x2 Dx1 C 2x2 D(a)13x1 2x2 Dx1 C 2x2 D(b)x2x22l21123l1x13x1l1(a)(b)FIGURE 2 (a) No solution. (b) Infinitely many solutions.Figures 1 and 2 illustrate the following general fact about linear systems, to beverified in Section 1.2.
01 000200010271308615 CH01 p001-092605/26/201215:00 PMPage 6Linear Algebra and Differential EquationsA system of linear equations hasaPe1. no solution, or2. exactly one solution, or3. infinitely many solutions.A system of linear equations is said to be consistent if it has either one solution orinfinitely many solutions; a system is inconsistent if it has no solution.nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribMatrix NotationThe essential information of a linear system can be recorded compactly in a rectangulararray called a matrix. Given the systemx12x2 C x3 D02x28x3 D84x1 C 5x2 C 9x3 D9(3)with the coefficients of each variable aligned in columns, the matrix231 2 14 02854 5 9tisDis called the coefficient matrix (or matrix of coefficients) of the system (3), and231 2 1 04 028 854 5 9 9(4)is called the augmented matrix of the system. (The second row here contains a zerobecause the second equation could be written as 0 x1 C 2x2 8x3 D 8.) An augmentedmatrix of a system consists of the coefficient matrix with an added column containingthe constants from the right sides of the equations.The size of a matrix tells how many rows and columns it has. The augmented matrix(4) above has 3 rows and 4 columns and is called a 3 4 (read “3 by 4”) matrix. If mand n are positive integers, an m n matrix is a rectangular array of numbers with mrows and n columns. (The number of rows always comes first.) Matrix notation willsimplify the calculations in the examples that follow.Solving a Linear SystemThis section and the next describe an algorithm, or a systematic procedure, for solvinglinear systems. The basic strategy is to replace one system with an equivalent system(i.e., one with the same solution set) that is easier to solve.Roughly speaking, use the x1 term in the first equation of a system to eliminatethe x1 terms in the other equations. Then use the x2 term in the second equation toeliminate the x2 terms in the other equations, and so on, until you finally obtain a verysimple equivalent system of equations.Three basic operations are used to simplify a linear system: Replace one equationby the sum of itself and a multiple of another equation, interchange two equations, andmultiply all the terms in an equation by a nonzero constant. After the first example, youwill see why these three operations do not change the solution set of the system.
01 000200010271308615 CH01 p001-09205/26/201215:00 PMCHAPTER 1Page 7Linear Equations in Linear Algebra7EXAMPLE 1 Solve system (3).SOLUTION The elimination procedure is shown here with and without matrix notation,and the results are placed side by side for comparison:aPex12x2 C x3 D2x2 8x3 D4x1 C 5x2 C 9x3 D089214 0422530859189nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribKeep x1 in the first equation and eliminate it from the other equations. To do so, add 4times equation 1 to equation 3. After some practice, this type of calculation is usuallyperformed mentally:4x1 8x2 C 4x3 D4x1 C 5x2 C 9x3 D4 Œequation 1 WC Œequation 3 WŒnew equation 3 W3x2 C 13x3 D099The result of this calculation is written in place of the original third equation:x12x2 C x3 D2x28x3 D3x2 C 13x3 D08921400308592 1283 13Now, multiply equation 2 by 1 2 in order to obtain 1 as the coefficient for x2 . (Thiscalculation will simplify the arithmetic in the next step.)Dx1tis2x2 C x3 Dx24x3 D3x2 C 13x3 D04921400304592 1143 13Use the x2 in equation 2 to eliminate the 3x2 in equation 3. The “mental” computationis3 Œequation 2 W3x2 12x3 D 12C Œequation 3 W3x2 C 13x3 D 9[new equation 3 Wx3 D3The new system has a triangular form:1x12x2 C x3 D 0x2 4x3 D 4x3 D 32140021014130453Eventually, you want to eliminate the 2x2 term from equation 1, but it is more efficientto use the x3 in equation 3 first, to eliminate the 4x3 and Cx3 terms in equations 2 and 1.The two “mental” calculations are4 Œeq. 3 WC Œeq. 2 WŒnew eq. 2 W1 Thex2x24x3 D 124x3 D 4D 16x3 D32x2 C x3 D01 Œeq. 3 WC Œeq. 1 WŒnew eq. 1 Wx1x12x2intuitive term triangular will be replaced by a precise term in the next section.D3
01 000200010271308615 CH01 p001-092805/26/201215:00 PMPage 8Linear Algebra and Differential EquationsIt is convenient to combine the results of these two operations:x12x2x2aPeD 3D 16x3 D 3214002100013316 53nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribNow, having cleaned out the column above the x3 in equation 3, move back to the x2 inequation 2 and use it to eliminate the 2x2 above it. Because of the previous work withx3 , there is now no arithmetic involving x3 terms. Add 2 times equation 2 to equation 1and obtain the system:823ˆD 291 0 0 29 x1401 0 16 5x2D 16:̂00 13x D 33The work is essentially done. It shows that the only solution of the original system is.29; 16; 3/. However, since there are so many calculations involved, it is a good practiceto check the work. To verify that .29; 16; 3/ is a solution, substitute these values intothe left side of the original system, and compute:.29/(29, 16, 3)9The results agree with the right side of the original system, so .29; 16; 3/ is a solutionof the system.tisDEach of the original equationsdetermines a plane in threedimensional space. The point.29; 16; 3/ lies in all three planes.2.16/ C .3/ D 29 32 C 3 D 02.16/ 8.3/ D 32 24 D 84.29/ C 5.16/ C 9.3/ D 116 C 80 C 27 DExample 1 illustrates how operations on equations in a linear system correspond tooperations on the appropriate rows of the augmented matrix. The three basic operationslisted earlier correspond to the following operations on the augmented matrix.ELEMENTARY ROW OPERATIONS1. (Replacement) Replace one row by the sum of itself and a multiple of anotherrow.22. (Interchange) Interchange two rows.3. (Scaling) Multiply all entries in a row by a nonzero constant.Row operations can be applied to any matrix, not merely to one that arises as theaugmented matrix of a linear system. Two matrices are called row equivalent if thereis a sequence of elementary row operations that transforms one matrix into the other.It is important to note that row operations are reversible. If two rows are interchanged, they can be returned to their original positions by another interchange. If arow is scaled by a nonzero constant c , then multiplying the new row by 1 c producesthe original row. Finally, consider a replacement operation involving two rows—say,rows 1 and 2—and suppose that c times row 1 is added to row 2 to produce a new row 2.To “reverse” this operation, add c times row 1 to (new) row 2 and obtain the originalrow 2. See Exercises 29–32 at the end of this section.2Acommon paraphrase of row replacement is “Add to one row a multiple of another row.”
01 000200010271308615 CH01 p001-09205/26/201215:00 PMCHAPTER 1Page 9Linear Equations in Linear Algebra9aPeAt the moment, we are interested in row operations on the augmented matrix of asystem of linear equations. Suppose a system is changed to a new one via row operations. By considering each type of row operation, you can see that any solution of theoriginal system remains a solution of the new system. Conversely, since the originalsystem can be produced via row operations on the new system, each solution of the newsystem is also a solution of the original system. This discussion justifies the followingstatement.nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribIf the augmented matrices of two linear systems are row equivalent, then the twosystems have the same solution set.Though Example 1 is lengthy, you will find that after some practice, the calculationsgo quickly. Row operations in the text and exercises will usually be extremely easy toperform, allowing you to focus on the underlying concepts. Still, you must learn toperform row operations accurately because they will be used throughout the text.The rest of this section shows how to use row operations to determine the size of asolution set, without completely solving the linear system.Existence and Uniqueness QuestionstisDSection 1.2 will show why a solution set for a linear system contains either no solutions,one solution, or infinitely many solutions. Answers to the following two questions willdetermine the nature of the solution set for a linear system.To determine which possibility is true for a particular system, we ask two questions.TWO FUNDAMENTAL QUESTIONS ABOUT A LINEAR SYSTEM1. Is the system consistent; that is, does at least one solution exist?2. If a solution exists, is it the only one; that is, is the solution unique?These two questions will appear throughout the text, in many different guises. Thissection and the next will show how to answer these questions via row operations on theaugmented matrix.EXAMPLE 2 Determine if the following system is consistent:x12x2 C x3 D2x2 8x3 D4x1 C 5x2 C 9x3 D089SOLUTION This is the system from Example 1. Suppose that we have performed therow operations necessary to obtain the triangular form23x1 2x2 C x3 D 012 1 04014 45x2 4x3 D 40 0 1 3x D33At this point, we know x3 . Were we to substitute the value of x3 into equation 2, wecould compute x2 and hence could determine x1 from equation 1. So a solution exists;the system is consistent. (In fact, x2 is uniquely determined by equation 2 since x3 has
01 000200010271308615 CH01 p001-0921005/26/201215:00 PMPage 10Linear Algebra and Differential Equationsonly one possible value, and x1 is therefore uniquely determined by equation 1. So thesolution is unique.)aPeEXAMPLE 3 Determine if the following system is consistent:x24x3 D 83x2 C 2x3 D 15x18x2 C 7x3 D 1(5)nstioluSoeng alni sar ReLe r r ionoftOuon trs Norib2x1SOLUTION The augmented matrix is2042513842738151To obtain an x1 in the first equation, interchange rows 1 and 2:2240531824731851To eliminate the 5x1 term in the third equation, add 5 2 times row 1 to row 3:tisD22400311 2242318 53 2Next, use the x2 term in the second equation to eliminate thethird equation. Add 1 2 times row 2 to row 3:22400310240318 55 2(6).1 2/x2 term from the(7)The augmented matrix is now in triangular form. To interpret it correctly, go back toequation notation:2x1This system is inconsistentbecause there is no point that liesin all three planes.3x2 C 2x3 D 1x24x3 D 80 D 5 2(8)The equation 0 D 5 2 is a short form of 0x1 C 0x2 C 0x3 D 5 2. This system in triangular form obviously has a built-in contradiction. There are no values of x1 ; x2 ; x3 thatsatisfy (8) because the equation 0 D 5 2 is never true. Since (8) and (5) have the samesolution set, the original system is inconsistent (i.e., has no solution).Pay close attention to the augmented matrix in (7). Its last row is typical of aninconsistent system in triangular form.
01 000200010271308615 CH01 p001-09205/26/201215:00 PMCHAPTER 1Page 11Linear Equations in Linear Algebra11NUMERICAL NOTEaPeIn real-world problems, systems of linear equations are solved by a computer. Fora square coefficient matrix, computer programs nearly always use the eliminationalgorithm given here and in Section 1.2, modified slightly for improved accuracy.The vast majority of linear algebra problems in business and industry aresolved with programs that use floating point arithmetic. Numbers are representedas decimals :d1 dp 10r , where r is an integer and the number p of digits tothe right of the decimal point is usually between 8 and 16. Arithmetic with suchnumbers typically is inexact, because the result must be rounded (or truncated) tothe number of digits stored. “Roundoff error” is also introduced when a numbersuch as 1 3 is entered into the computer, since its decimal representation must beapproximated by a finite number of digits. Fortunately, inaccuracies in floatingpoint arithmetic seldom cause problems. The numerical notes in this book willoccasionally warn of issues that you may need to consider later in your career.nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribPRACTICE PROBLEMSThroughout the text, practice problems should be attempted before working the exercises. Solutions appear after each exercise set.1. State in words the next elementary row operation that should be performed on thesystem in order to solve it. [More than one answer is possible in (a).]tisDa. x1 C 4x2x22x3 C 8x4 D 127x3 C 2x4 D 45x3x4 D 7x3 C 3x4 D 5b. x13x2 C 5x32x4 D0x2 C 8x3D42x3D3x4 D12. The augmented matrix of a linear system has been transformed by row operationsinto the form below. Determine if the system is consistent.231 5 264047 250 0 5 03. Is .3; 4; 2/ a solution of the following system?5x1x2 C 2x3 D2x1 C 6x2 C 9x3 D7x1 C 5x2 3x3 D7074. For what values of h and k is the following system consistent?2x1x2 D h6x1 C 3x2 D k
01 000200010271308615 CH01 p001-0921205/26/201215:00 PMPage 12Linear Algebra and Differential Equations1.1 EXERCISES1.aPeSolve each system in Exercises 1–4 by using elementary rowoperations on the equations or on the augmented matrix. Followthe systematic elimination procedure described in this section.x1 C 5x2 D2x17x2 D752. 3x1 C 6x2 D3160610. 40031000010230137677252Solve the systems in Exercises 11–14.5x1 C 7x2 D 10x2 C 5x3 D11.x1 C 4x2 C 3x3 D42nstioluSoeng alni sar ReLe r r ionoftOuon trs Norib3. Find the point .x1 ; x2 / that lies on the line x1 C 2x2 D 4 andon the line x1 x2 D 1. See the figure.x22x1 – x2 12x1 C 7x2 C x3 D12.x15x2 C 4x3 D32x1 C x2 C 7x3 D12x113.x17x2 C 3x3 Dx18x2 C 5x3 D26x3 D82x3 D414. 2x14. Find the point of intersection of the lines x1 C 2x2 Dand 3x1 2x2 D 11323x3 D2x1 C 2x2 C 9x3 Dx1 2x2 42x2 C 2x3 D3x1 C 6x273Determine if the systems in Exercises 15 and 16 are consistent.Do not completely solve the systems.In Exercises 7–10, the augmented matrix of a linear system hasbeen reduced by row operations to the form shown. In each case,continue the appropriate row operations and describe the solutionset of the original system.23173460113777. 640001500122315400601010778. 64003005000202311005601207779. 640013250001417. Do the three lines 2x1 C 3x2 D 1, 6x1 C 5x2 D 0, and2x1 5x2 D 7 have a common point of intersection? Explain.15.x16x2x2tisDConsider each matrix in Exercises 5 and 6 as the augmented matrixof a linear system. State in words the next two elementary rowoperations that should be performed in the process of solving thesystem.3214307601406775. 64001025000153216401602704776. 6400123500412D54x3 C x4 D 0x1 C 6x2 C x3 C 5x4 D 3x2 C 5x3 C 4x4 D 016.2x14x4 D10x3 C 4x4 D13x2 C 3x3D3x1 C 2x2 C 3x3 C x4 D0518. Do the three planes 2x1 C 4x2 C 4x3 D 4, x2 2x3 D 2,and 2x1 C 3x2 D 0 have at least one common point of intersection? Explain.In Exercises 19–22, determine the value(s) of h such that thematrix is the augmented matrix of a consistent linear system. 1h41h519.20.368286 142412h21.22.3h6263In Exercises 23 and 24, key statements from this section areeither quoted directly, restated slightly (but still true), or alteredin some way that makes them false in some cases. Mark eachstatement True or False, and justify your answer. (If true, give the
01 000200010271308615 CH01 p001-09205/26/201215:00 PMCHAPTER 1aPeapproximate location where a similar statement appears, or referto a definition or theorem. If false, give the location of a statementthat has been quoted or used incorrectly, or cite an example thatshows the statement is not true in all cases.) Similar true/falsequestions will appear in many sections of the text.23. a. Every elementary row operation is reversible.b. A 5 6 matrix has six rows.d. Two fundamental questions about a linear system involveexistence and uniqueness.24. a. Two matrices are row equivalent if they have the samenumber of rows.b. Elementary row operations on an augmented matrix neverchange the solution set of the associated linear system.c. Two equivalent linear systems can have different solutionsets.d. A consistent system of linear equations has one or moresolutions.An important concern in the study of heat transfer is to determinethe steady-state temperature distribution of a thin plate when thetemperature around the boundary is known. Assume the plateshown in the figure represents a cross section of a metal beam,with negligible heat flow in the direction perpendicular to theplate. Let T1 ; : : : ; T4 denote the temperatures at the four interiornodes of the mesh in the figure. The temperature at a node isapproximately equal to the average of the four nearest nodes—tothe left, above, to the right, and below.3 For instance,T1 D .10 C 20 C T2 C T4 / 4;26. Suppose the system below is consistent for all possible valuesof f and g . What can you say about the coefficients c andd ? Justify your answer.2x1 C 4x2 D f27. Suppose a, b , c , and d are constants such that a is not zeroand the system below is consistent for all possible values off and g . What can you say about the numbers a, b , c , andd ? Justify your answer.ax1 C bx2 D f13In Exercises 29–32, find the elementary row operation that transforms the first matrix into the second, and then find the reverserow operation that transforms the second matrix into the first.23 2302531635 5, 4 135529. 4 131602523 2313413426 5, 4 026530. 4 005 1001223 2312101210528 5, 4 0528531. 4 04136071623 2312501250132 5, 4 0132532. 4 004127000 15tisD25. Find an equation involving g , h, and k that makesthis augmented matrix correspond to a consistent system:32147g4 035h5259kcx1 C dx2 D gLinear Equations in Linear AlgebranstioluSoeng alni sar ReLe r r ionoftOuon trs Noribc. The solution set of a linear system involving variablesx1 ; : : : ; xn is a list of numbers .s1 ; : : : ; sn / that makes eachequation in the system a true statement when the valuess1 ; : : : ; sn are substituted for x1 ; : : : ; xn , respectively.Page 1310 10 or 4T120 20 124330 30 T2T4 D 3040 40 33. Write a system of four equations whose solution gives estimates for the temperatures T1 ; : : : ; T4 .34. Solve the system of equations from Exercise 33. [Hint: Tospeed up the calculations, interchange rows 1 and 4 beforestarting “replace” operations.]cx1 C dx2 D g28. Construct three different augmented matrices for linear systems whose solution set is x1 D 3, x2 D 2, x3 D 1.3 SeeFrank M. White, Heat and Mass Transfer (Reading, MA:Addison-Wesley Publishing, 1991), pp. 145–149.SOLUTIONS TO PRACTICE PROBLEMS1. a. For “hand computation,” the best choice is to interchange equations 3 and 4.Another possibility is to multiply equation 3 by 1 5. Or, replace equation 4 byits sum with 1 5 times row 3. (In any case, do not use the x2 in equation 2 toeliminate the 4x2 in equation 1. Wait until a triangular form has been reached andthe x3 terms and x4 terms have been eliminated from the first two equations.)
01 000200010271308615 CH01 p001-0921405/26/201215:00 PMPage 14Linear Algebra and Differential EquationsaPeb. The system is in triangular form. Further simplification begins with the x4 in thefourth equation. Use the x4 to eliminate all x4 terms above it. The appropriatestep now is to add 2 times equation 4 to equation 1. (After that, move to equation3, multiply it by 1 2, and then use the equation to eliminate the x3 terms aboveit.)2. The system corresponding to the augmented matrix isSince .3; 4; 2/ satisfies the firsttwo equations, it is on the line ofthe intersection of the first twoplanes. Since .3; 4; 2/ does notsatisfy all three equations, it doesnot lie on all three planes.620The third equation makes x3 D 0, which is certainly an allowable value for x3 . Aftereliminating the x3 terms in equations 1 and 2, you could go on to solve for uniquevalues for x2 and x1 . Hence a solution exists, and it is unique. Contrast this situationwith that in Example 3.3. It is easy to check if a specific list of numbers is a solution. Set x1 D 3, x2 D 4, andx3 D 2, and find that5.3/.4/ C 2. 2/ D2.3/ C 6.4/ C 9. 2/ D7.3/ C 5.4/ 3. 2/ D1544D76 C 24 18 D 021 C 20 C 6 D 5Although the first two equations are satisfied, the third is not, so .3; 4; 2/ is not asolution of the system. Notice the use of parentheses when making the substitutions.They are strongly recommended as a guard against arithmetic errors.4. When the second equation is replaced by its sum with 3 times the first equation, thesystem becomestisDnstioluSoeng alni sar ReLe r r ionoftOuon trs Norib(3, 4, –2)x1 C 5x2 C 2x3 D4x2 7x3 D5x3 D2x1x2 D h0 D k C 3hIf k C 3h is nonzero, the system has no solution. The system is consistent for anyvalues of h and k that make k C 3h D 0.1.2 ROW REDUCTION AND ECHELON FORMSThis section refines the method of Section 1.1 into a row reduction algorithm that willenable us to analyze any system of linear equations.1 By using only the first part ofthe algorithm, we will be able to answer the fundamental existence and uniquenessquestions posed in Section 1.1.The algorithm applies to any matrix, whether or not the matrix is viewed as anaugmented matrix for a linear system. So the first part of this section concerns anarbitrary rectangular matrix and begins by introducing two important classes of matricesthat include the “triangular” matrices of Section 1.1. In the definitions that follow, anonzero row or column in a matrix means a row or column that contains at least onenonzero entry; a leading entry of a row refers to the leftmost nonzero entry (in a nonzerorow).1 Thealgorithm here is a variant of what is commonly called Gaussian elimination. A similar eliminationmethod for linear systems was used by Chinese mathematicians in about 250 B.C. The process was unknownin Western culture until the nineteenth century, when a famous German mathematician, Carl Friedrich Gauss,discovered it. A German engineer, Wilhelm Jordan, popularized the algorithm in an 1888 text on geodesy.
01 000200010271308615 CH01 p001-09205/26/201215:00 PMCHAPTER 1DEFINITIONPage 15Linear Equations in Linear Algebra15A rectangular matrix is in echelon form (or row echelon form) if it has thefollowing three properties:aPe1. All nonzero rows are above any rows of all zeros.2. Each leading entry of a row is in a column to the right of the leading entry ofthe row above it.3. All entries in a column below a leading entry are zeros.nstioluSoeng alni sar ReLe r r ionoftOuon trs NoribIf a matrix in echelon fo
by R. Kent Nagle, Edward B. Saff and Arthur David Snider Linear Algebra & Differential Equations CFi-viii : age Pearson Learning Solutions Not for Resale Or Distribution. 00_000200010271308615_CH00_FM_pi-viii 05/28/2012 16:20 PM Page 8 Pearson Learning Solutions Not for Or Resale Distribution. 1 .
![No, David! (David Books [Shannon]) E Book](/img/65/no-20david-20david-20books-20shannon-20e-20book.jpg)