WIXLIB

Introduction to Computer Programming withMATLAB Calculation and ProgrammingErrorsSelis Önel, PhD

Today you will learn Numbers, Significant figuresError analysisAbsolute errorRelative errorChopping off versus Rounding offSelisÖnel 2

Significant Figures (Digits) A concept developed to formally designate the reliability of a numerical valueDigits of a number that can be used with confidenceZeros are not always significant figures depending on whetherthe zeros are known with confidenceThe number of significant digits in an answer to a calculationwill depend on the number of significant digits in the given data.Approximate calculations (order-of-magnitude estimates)always result in answers with only one or two significant digits.SelisÖnel 3

Significant Figures (Digits)Value# of significiant figuresValue# of significiant 85645300if 4.53x104 352.1485745945300if 4.530x104 452.1485000945300if 4.5300x104 5SelisÖnel 4

Zeros A. placed before other digits are not significant; 0.051 hastwo significant digits.B. placed between other digits are always significant;6002 kg has four significant digits.C. placed after other digits but behind a decimal point aresignificant; 2.40 has three significant digits.D. at the end of a number are significant only if they arebehind a decimal point as in C. Otherwise, it isimpossible to tell if they are significant.SelisÖnel 5

D. Zeros at the end of a number 3200 it is not clear if the zeroes are significant or not.The number of significant digits in 3200 is at least two, butcould be three or four.To avoid uncertainty, use scientific notation to placesignificant zeroes behind a decimal point: 3.200x103 has four significant digits 3.20x103 has three significant digits 3.2 x103 has two significant digitsSelisÖnel 6

Significant Digits in Multiplication,Division, Trig. functions, etc # of significant digits in an answer the least number ofsignificant digits in any one of the numbers beingmultiplied, divided etc. Ex: sin(kx), where k 0.081 m-1 (two significant digits) andx 5.21 m (three significant digits), the answer shouldhave two significant digits. Remember: Whole numbers have essentially an unlimitednumber of significant digits. Ex: if a hair dryer uses 1.4 kW of power, then 2 identicalhairdryers use 2.8 kW:1.4 kW {2 sig.dig.} x2 {unlimited sig.dig.} 2.8 kW {2 sig.dig.}SelisÖnel 7

Significant Digits in Addition andSubtraction number of decimal places (not significant digits) inthe answer the least number of decimal places inany of the numbers being added or subtracted.Example:5.67 J (two decimal places)1.1 J (one decimal place)0.9378 J (four decimal places)7.7 J (one decimal place)SelisÖnel 8

When doing multi-step calculations Keep at least one more significant digit in intermediateresults than needed in your final answer.Example:If a final answer requires two significant digits, then carry atleast three significant digits in calculations.If you round-off all your intermediate answers to only twodigits, you are discarding the information contained in thethird digit, and as a result the second digit in your final answermight be incorrect.This phenomenon is known as "round-off error")SelisÖnel 9

THINGS NOT TO DO! Writing more digits in a finalanswer than justified by thenumber of digits in the data. Rounding-off, say, to two digitsin an intermediate answer, andthen writing three digits in thefinal answer.SelisÖnel 10

Exercises1) ekt ?, where k 0.0286 yr-1, and t 15 yr2) ab/c ?, where a 256 J, b 33.56 J, and c 11.423) x y z ?, where x 48.1, y 77, and z 65.7894) m - n - p ?, where m 25.6, n 21.1, and p 2.43SelisÖnel 11

Exercises1) ekt ?, where k 0.0286 yr-1, and t 15 yr.[Ans. 0.4290]2) ab/c ?, where a 256 J, b 33.56 J, and c 11.42[Ans. 9.811 x 104 J2 ]3) x y z ?, where x 48.1, y 77, and z 65.789[Ans. 191]4) m - n - p ?, where m 25.6, n 21.1, and p 2.43[Ans. 2.1]SelisÖnel 12

Machine Numbers We do arithmetic using the decimal (base10) number system Computers do arithmetic using the binary(base 2) number system Computers convert the numbers we enterin base 10 to base 2, performs base 2arithmetic and then translates the answerto base 10 before it displays it as a resultSelisÖnel 13

Base 10 and Base 2 NumbersSelisÖnel Reference: Gilat, Subramaniam: Numerical Methods with Matlab14

Base 10 and Base 2 NumbersSelisÖnel Reference: Gilat, Subramaniam: Numerical Methods with Matlab15

Machine Numbers Computers use normalized floating-pointbinary representation for real numbers. This means mathematical quantity X is notactually stored in the computer. Instead computer stores: X q x 2nq: mantissa, where ½ q 1n: exponentSelisÖnel 16

Machine NumbersSelisÖnel Reference: Gilat, Subramaniam: Numerical Methods with Matlab17

Quality control in computing We are problem solvingengineers and our workwill be used by clients andsponsors, so our programsmust be reliable When preparing orexecuting a programERRORS will occur called BUGS in computerjargon (remember AdmiralGrace Hopper,1945)SelisÖnel 18

Quality control in computingThe fact that acomputer programprints out information isno guarantee thatthese answers arecorrect!SelisÖnel 19

When running or developing a program: BUGS Syntax errors: Violate rules of language such as spelling,number formation, etc. Ex: REED vs READ Link or build errors: Occur during link phase. Ex:Misspelling the name of an intrinsic function Run-time errors: Occur during program execution. Ex:Insufficient number of data entries for the number ofvariables in an input statement Logic errors: Occur due to faultyprogram logic. Dangerous becauseprogram may work properly but theoutput will be incorrect!SelisÖnel 20

Debugging and Debug: Correct known errorsIf a program runs and printsout reasonable results Do I know it is correct?You need to TEST the programand check the resultsSelisÖnel 21

Testing: To ensure program is correctDebug and test modules prior to integrating theminto the total program Module tests: Use sample input data to test eachfunction called in the program Developmental tests: Perform a test afterintegrating each module (function) one by one Whole system tests: After the whole programis assembled run the program using: Typical data Unusual but valid data Incorrect data to check if the program canhandle errorsSelisÖnel 22

Accuracy and Precision Accuracy how closely acomputed or measured valueagrees with the true value Precision how closelyindividual computed ormeasured values agree witheach otherSelisÖnel 23

Error AnalysisAbsolute error is:An approximation errorcan occur because: Measurement of datais not precise (due tothe instruments), or Approximations areused instead of thereal data (e.g., 3.14instead of π)If a 0, the relative error is:Percent error is:SelisÖnel 24

Approximation Errors Round-off errors Truncation errorsSelisÖnel 25

Round-off Errors Due to use of numbers with limited significant figures torepresent exact numbers.ex: e, π, 7 (no fixed number of significant figures)ex: Computer base-2 representation cannot preciselyrepresent certain exact base-10 numbers.ex: 1/10 0.00011two actual number in the computer may undergo chopping orrounding of the last digit Computer’s representation of real numbers is limited tothe fixed precision of the mantissaSelisÖnel 26

Round-off ErrorsDouble-precisionuses 16 digits format long e pians 3.141592653589793e 000 sqrt(7)ans 2.645751311064591e 000Floating-point Representation: Used for fractional quantitiesin computers.m·bx m: mantissa (significand)b: base of number systemx: exponentMantissa holds only a finite number of significant figuresSelisÖnel 27

Truncation ErrorsDerivative of velocity of a carTruncation errordv v v(ti 1 ) v(ti ) (or discretization error) :dt tti 1 ti Due to use of approximations torepresent exact mathematical procedures Introduced when a more complicated mathematicalexpression is replaced with a more elementary formula Due to using finite number of steps in computation Present even with infinite-precision arithmetic, because itis caused by truncation of the infinite Taylor series to formthe algorithmSelisÖnel 28

Truncation Errors and Taylor SeriesWhy is Taylor series important in the study ofNumerical Methods?- Provides ways to predict a function value at one point interms of the function value and its derivatives at anotherpoint- States that any smooth function can be approximated asa polynomialReference: S. C. Chapra and R. P. Canale, Numerical Methods for Engineers, 3rd Ed., WCB/McGrawHill, 1998, p.79SelisÖnel 29

Truncation Errors and Taylor Series A Taylor series of a real (or complex) function f(x) isinfinitely differentiable in a neighborhood of a real (orcomplex) number a, i.e. it is the power series:or f(x) is usually equal to its Taylor series evaluated at x forall x sufficiently close to a If a 0 Maclaurin seriesSelisÖnel 30

Why Use Approximating Functions? Replace f(x) (ex: transcendental functions ln x, sin x, erfx, ) with g(x) (ex: a power series) which can handlearithmetic operations Ex:4682nxxxxe x 1 x 2 . .2! 3! 4!n!Using just 5 terms to simplify gives:2468xxxe 1 x 2! 3! 4!x22SelisÖnel 31

Example Problem (Mathews & Fink p.26)12Given that e dx 0.544987104184 px2determine the accuracy0of the approximation obtained by replacing the integrand f ( x) ex2468xxxwith the truncated Taylor series P8 ( x) 1 x 2 2! 3! 4!Term by term integration gives:x 12 xxx xxxx 2 0 1 x 2! 3! 4! dx x 3 5(2!) 7(3!) 9(4!) x 01 11112,109, 491 0.544986720817 pnew2 24 320 5376 110,592 3,870, 720124683p pnewerror % 7.03442 10 7p57910 510 6 error % 22The approximation pnew agrees with the true answer p tofive significant figuresSelisÖnel 32

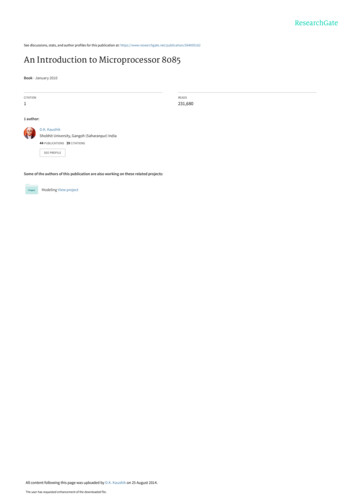
y and pExample Problem (Mathews & Fink p.26)The graphs show the area under the curves between x 0 and 0.55y ex24.5p 1 x 2 x 4/2! x 6/3! x .2x33SelisÖnel

Chopping off versus Rounding off Consider real number p expresses in normalizeddecimal form:p 0.d1d2d3.dkdk 1.*10nwhere 1 d1 9 andfor j 1, 0 dj 9I. CHOPPINGk: maximum number of decimal digitscarried in the floating-pointcomputations of a computer.pchopped 0.d1d2d3.dk*10nSelisÖnel chopped floating-pointrepresentation of p34

Chopping off versus Rounding off Consider real number p expresses in normalizeddecimal form:p 0.d1d2d3.dkdk 1.*10nwhere 1 d1 9 andfor j 1, 0 dj 9I. ROUNDINGk: maximum number of decimal digitscarried in the floating-pointcomputations of a computer.prounded 0.d1d2d3.rk*10nrounded floating-pointrepresentation of prk : last digit is obtained by rounding the number dkdk 1dk 2.to the nearest integer35SelisÖnel

Ex: Rounding vs ChoppingReal number22p 3.142857142857142857.76-digit representationPchopped 0.314285 * 101prounded 0.314286 * 101Essentially all computers use some form of rounded floatingpoint representation methodSelisÖnel 36

Loss of significanceThe final computed answer may be different depending on yourcalculation stepsEx1: Consider functions f(x) and g(x)f ( x ) x( x 1 g( x ) x)xx 1 SelisÖnel x37

Loss of significance Ex1 cont.df ( x ) x( x 1 x)xg( x ) x 1 xFunctions f(x) and g(x) are identical:f (x) x(x 1 x ( x )(x 1 x)xx )2 x 1)2 (x 1 x 1 xSelisÖnel xx 1 x g( x )38

Loss of significance Ex1 cont.dCalculate f(500) and g(500):f (500) 500( 501 500 ) 500(22.3830 22.3607) 500(0.0223) 11.1500g (500) 500501 500500500 11.174822.3830 22.3607 44.7437Matlab results (format long) with 15decimal digitsf(500) 11.174755300746853g(500) 11.174755300747199SelisÖnel Hand calculation with 4 decimaldigitsf(500) 11.1500g(500) 11.174839

Loss of significance Ex2Compare results of f(0.01) and g(0.01) using 6 digits and roundingex 1 xf (x) x2and1 x x2g( x ) 2 6 24g(x) is the Taylor polynomial of degree n 2 for f(x) expanded about x 0e0.01 1 0.01 1.010050 1 0.01f (0.01) 0.52(0.01)0.00011 0.01 0.001g (0.01) 0.5 0.001667 0.000004 0.5016712624Matlab results for x 0.01;f (exp(x) -1-x)/x 2 f 0.501670841679489g 1/2 x/6 x 2/24 g 0.5016708333333330.501671 g(0.01) contains less error and is the same as that obtained40by rounding the true answer 0.501670841679489 to six digits.