WIXLIB

Safety Control of a Class of Stochastic Order Preserving Systems withApplication to Collision Avoidance near Stop SignsMojtaba Forghani1 , John M. McNew2 , Daniel Hoehener1 and Domitilla Del Vecchio1Abstract— In this paper, we consider the problem of keepingthe state of a system outside of an undesired set of stateswith probability at least P. We focus on a class of orderpreserving systems with a constant input disturbance that isextracted from a known probability distribution. Leveragingthe structure of the system, we construct an explicit supervisorthat guarantees the system state to be kept outside the undesiredset with at least probability P. We apply this supervisor to acollision avoidance problem, where a semi-autonomous vehicleis engaged in preventing a rear-end collision with a precedinghuman-driven vehicle, while stopping at a stop sign. We applythe designed supervisor in simulations in which the precedingvehicle trajectories are taken from a test data set. Using thisdata, we demonstrate experimentally that the probability ofpreventing a rear-end collision while stopping at the stop signis at least P, as expected from theory. The simulation resultsfurther show that this probability is very close to P, indicatingthat the supervisor is not conservative.I. INTRODUCTIONThe problem of designing control strategies that guaranteethe safety of a system, that is, avoidance of a dangerousset of states, has been studied for many years in thecontext of deterministic systems, chiefly by [1]–[3]. Thisproblem has been solved by deriving the Hamilton-JacobiBellman equation whose solutions describe the boundary ofthe maximal safe controlled invariant set. While in generalcomputing this set is computationally difficult, a number ofground transportation systems can be modeled by a specialclass of systems, called order preserving systems, that allowcomputationally efficient solutions [4]–[8].When the system model is stochastic, the problem ofdesigning safety-enforcing controllers has been addressedonly more recently. In particular, the maximum achievablesafety probability for a given initial state for stochasticnonlinear and hybrid systems has been investigated in [9].In [10] and [11], the corresponding control policy thatguarantees this maximal safety probability is also provided.Safety for a given probability P, which is our primary goalin this work, for a particular class of systems has beenaddressed in [20]. This problem is of practical relevance ina number of application scenarios, including the design ofon-board driver-assist systems that warn/override the driverto guarantee a prescribed safety level. The application of ourThis work was supported by NSF under the award #11618931 Mojtaba Forghani, Daniel Hoehener and Domitilla Del Vecchio are withthe Department of Mechanical Engineering, MIT, 77 Massachusetts Avenue,Cambridge, MA. mojtaba@mit.edu, hoehener@mit.edu,ddv@mit.edu2 John M. McNew is with Toyota Technical Center, 1555 WoodridgeAvenue, Ann Arbor, MI. john.mcnew@tema.toyota.comalgorithms to collision avoidance scenarios near stop signsis the second goal of our work.The problem of preventing or mitigating collisions nearintersections (signaled or not) is a major focus of researchdue to the large number of collisions and fatalities that stilloccur today world-wide [12]. For example, in the UnitedStates, over the last several years an average of 21% of thefatalities and roughly 50% of the serious injuries have beenattributed to intersections [13]. In order to design driver-assistsystems that apply a warning or an override at the right timewhen the surrounding vehicles do not communicate, it isimportant to have a model of the behavior of these vehicles. Previously, deterministic models were considered forcontroller design, wherein the vehicle behavior was modeledthrough a set of modes with bounded disturbances capturingthe variability among and within drivers in each mode (see[4] and [5]). Since driver’s behavior and variability amongdrivers is better captured by probabilistic disturbances, weconsider here a model where the disturbance has a probabilitydistribution, which can be learned from data. This allows todesign warnings and overrides that are less conservative andcan guarantee a given probability of safety.In [14] and [15], HMMs (Hidden Markov Model) wereemployed as a stochastic model for driver behavior forestimation/prediction purposes. While these models providethe desired results for estimation/prediction tasks, giventheir complexity, they are less suited for real-time controlpurposes. In this paper, we therefore consider a simplermodel in which the continuous dynamics are order preservingand the disturbance inputs are constant parameters distributedaccording to a Gaussian probability distribution. With theseassumptions, we provide a control map that can be efficientlycomputed on-line for guaranteeing a given probability ofsafety P. We apply our algorithms to a collision avoidancescenario wherein one vehicle needs to stop at a stop signwhile preventing a collision with a preceding human-drivenvehicle. The model of the preceding vehicle is learned fromdata gathered from vehicles driving in Ann Arbor (MI).A different data set for the preceding vehicle trajectorieswas used in simulations to emulate the preceding vehicle.In these simulations, the following vehicle was supervisedthrough our control algorithm that provided overrides toensure a probability of safety P. Simulation results showthat the prescribed probability of safety P (and not morethan P) was indeed ensured validating the algorithms onexperimental data and demonstrating the non-conservatismof the approach.This paper is organized as follows. In Section II, we pro-

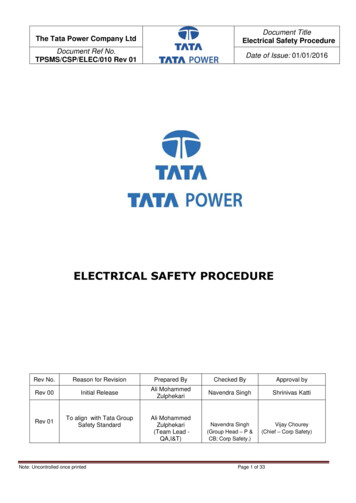
vide details of the stochastic model, introduce the collisionavoidance application, and formulate the control problems.In Section III, we solve the control problems and in SectionIV we provide the details of the implementation.II. STOCHASTIC MODELAssumption 2: System Σ2 is strict input/output orderpreserving with respect to the disturbance input and its flowφ 2 is continuous in all arguments.Assumption 3: The disturbance input is a constant withGaussian distribution, that is, d(t) : d N (µ, σ 2 ), for allt R .A. System ModelB. Application ScenarioWe start with some basic definitions.Definition 1: For all w, z Rn we have that w z (w z),if and only if wi zi (wi zi ) for all i {1, 2, ., n}, inwhich wi denotes the ith component of w. We denote thepiecewise continuous signal on U by S(U ) : R U . ForU Rm we define the partial order (strict partial order)by component-wise ordering for all times, that is, for allw, z S(U ) we have that w z (w z) provided w(t) z(t)(w(t) z(t)) for all t R . The map f : P Q is orderpreserving (strict order preserving) provided if for x, y Pwe have x y (x y), then f (x) f (y) ( f (x) f (y)).Definition 2: A continuous system is a collection Σ (X,U, , O, f , h), with state x X Rn , control input u U Rm , disturbance input d Rq , output y O X,vector field in the form of f : X U X, and outputmap h : X O.Definition 3: For Σ1 (X 1 ,U 1 , 1 , O1 , f 1 , h1 ) and Σ2 (X 2 ,U 2 , 2 , O2 , f 2 , h2 ), we define the parallel compositionΣ Σ1 Σ2 : (X,U, , O, f , h), in which X X 1 X 2 , U : U 1 U 2 , : 1 2 , O : O1 O2 , f : ( f 1 , f 2 ) and h : (h1 , h2 ).We denote the flow of a system Σ at time t R byφ (t, x, u, d), with initial condition x X, control input signalu S(U), and disturbance input signal d S( ). We alsodenote the ith component of the flow by φi (t, x, u, d).Definition 4: A continuous system Σ (X,U, , O, f , h)is called input/output order preserving (strict input/outputorder preserving) with respect to the control input signal,if the map h(φ (t, x, ·, d)) : S(U) O, for any fixed t, x andd, is order preserving (strict order preserving).Definition 5: A continuous system Σ (X,U, , O, f , h)is called input/output order preserving (strict input/outputorder preserving) with respect to the disturbance input signal,if the map h(φ (t, x, u, ·)) : S( ) O, for any fixed t, x andu, is order preserving (strict order preserving).In this paper, we consider system Σ Σ1 Σ2 , which is theparallel composition of Σ1 (X 1 ,U, 0,/ O1 , f 1 , h1 ) and Σ2 12222211(X , 0,/ , O , f , h ), where x X Rn , x2 X 2 Rn ,u U [um , uM ] Rm , with um Rm and uM Rm theminimal and the maximal control inputs for Σ1 , respectively,d R, y1 O1 , y2 O2 , h1 : X 1 O1 , h2 : X 2 O2 ,f 1 : X 1 U X 1 and f 2 : X 2 X 2 . Since 1 0/and U 2 0,/ we represent the flows of systems Σ1 and Σ211by φ (t, x , u) and φ 2 (t, x2 , d), respectively. The followingassumptions are made on system Σ .Assumption 1: System Σ1 is input/output order preserving with respect to the control input and its flow φ 1 iscontinuous in all arguments.We consider the scenario of two consecutive vehiclesapproaching a stop sign. We assume that the followingvehicle (FV) is equipped with the collision avoidance system,while the preceding vehicle (PV) is fully human driven. Weconsider two types of “collisions”: type (1), the rear-endcollision between the two vehicles; type (2), crossing the stopsign with a high velocity. We denote longitudinal positionand velocity of PV by x p and v p , respectively. Similarly, x fand v f are position and velocity of FV, respectively. Thelongitudinal position of the stop sign is St and the maximumallowable velocity of FV at the stop sign is vT . The minimumallowable distance between the two vehicles is δ 0. Thescenario is depicted in Figure 1.Fig. 1: Collision scenarios.The system model for the application scenario is given byΣapp : Σ1 Σ2 , where Σ1 and Σ2 are FV and PV, respectively.Hence, x1 (x f , v f )T , x2 (x p , v p )T , y1 x f , y2 x p ,h1 (x1 ) x f and h2 (x2 ) x p . The deceleration due to therolling resistance and the slope of the road of FV are ar andas , respectively. We let D denote the drag coefficient. Wealso assume that the speed of both vehicles is non-negative.The control input is u U R, and the disturbance input isd R. We define functions f 1 (x1 , u1 ) and f 2 (x2 , u2 ), whereu1 u and u2 d, as follows. i i if (x , u )if vi 0i i ifor i {1, 2}, f (x , u ) , (1)0if vi 0where v1 v f and v2 v p . Also, f 1 (x1 , u) and f 2 (x2 , d) are Tf 1 (x1 , u) v f , u Dv2f ar as ,(2a) f 2 (x2 , d) (v p , ax p bv p d)T .(2b)The term ax p bv p d is the acceleration of PV. More detailson this model are provided in Section IV. We assume thatd N (µ, σ 2 ), which is consistent with Assumption 3.Based on Assumption 1, the flow h1 (φ 1 (t, x1 , u)) 1φ1 (t, x1 , u) x f (t) must be order preserving with respect to