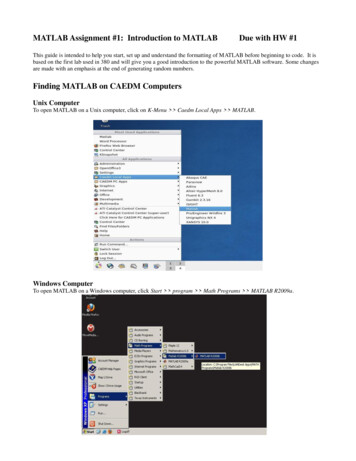
Transcription
MATLABLinear ProgrammingGreg Reese, Ph.DResearch Computing Support GroupAcademic Technology ServicesMiami University
MATLABLinear Programming 2010-2013 Greg Reese. All rights reserved2
OptimizationOptimization - finding value of a parameterthat maximizes or minimizes a function withthat parameter– Talking about mathematical optimization, notoptimization of computer code!– "function" is mathematical function, notMATLAB language function3
OptimizationOptimization– Can have multiple parameters– Can have multiple functions– Parameters can appear linearly ornonlinearly4
Linear programmingLinear programming Most often used kind of optimization Tremendous number of practicalapplications "Programming" means determiningfeasible programs (plans, schedules,allocations) that are optimal withrespect to a certain criterion and thatobey certain constraints5
Linear programmingA feasible program is a solution to alinear programming problem and thatsatisfies certain constraintsIn linear programming Constraints are linear inequalities Criterion is a linear expression– Expression called the objective function– In practice, objective function is oftenthe cost of or profit from some activity6
Linear programmingMany important problems ineconomics and management can besolved by linear programmingSome problems are so common thatthey're given special names7
Linear programmingDIET PROBLEMYou are given a group of foods, theirnutritional values and costs. You know howmuch nutrition a person needs.What combination of foods can you servethat meets the nutritional needs of a personbut costs the least?8
Linear programmingBLENDING PROBLEM–Closely relate to diet problemGiven quantities and qualities of availableoils, what is cheapest way to blend theminto needed assortment of fuels?9
Linear programmingTRANSPORTATION PROBLEMYou are given a group of ports or supply centers ofa certain commodity and another group ofdestinations or markets to which commodity mustbe shipped. You know how much commodity ateach port, how much each market must receive,cost to ship between any port and market.How much should you ship from each port to eachmarket so as to minimize the total shipping cost?10
Linear programmingWAREHOUSE PROBLEMYou are given a warehouse of known capacity andinitial stock size. Know purchase and selling priceof stock. Interested in transactions over a certaintime, e.g., year. Divide time into smaller periods,e.g., months.How much should you buy and sell each period tomaximize your profit, subject to restrictions that1. Amount of stock at any time can't exceed warehousecapacity2. You can't sell more stock than you have11
Linear programmingMathematical formulationThe variables x1, x2, . xn satisfy the inequalitiesa11x1 a12 x2 a1n xn b1a21x1 a22 x2 a2 n xn b2 am1 x1 am 2 x2 amn xn bmand x1 0, x2 0, . xn 0 . Find the set of valuesof x1, x2, . xn that minimizes (maximizes)x1 f1 x2 f 2 xn f nNote that apq and fi are known12
Linear programmingMathematical matrix formulationFind the value of x that minimizes (maximizes)fTx given that x 0 and Ax b, where a11 aA 21 am1a12 a1n b1 x1 f1 b x f a21 a21 22, b , x , and f 2 am 2 amn bx m n fn 13
Linear programmingGeneral procedure1. Restate problem in terms of equationsand inequalities2. Rewrite in matrix and vector notation3. Call MATLAB function linprog to solve14
Linear programmingExample - diet problemMy son's diet comes from the four basic food groups chocolate dessert, ice cream, soda, and cheesecake. Hechecks in a store and finds one of each kind of food,namely, a brownie, chocolate ice cream, Pepsi, and oneslice of pineapple cheesecake. Each day he needs atleast 500 calories, 6 oz of chocolate, 10 oz of sugar, and 8oz of fat. Using the table on the next slide that gives thecost and nutrition of each item, figure out how much heshould buy and eat of each of the four items he found inthe store so that he gets enough nutrition but spends aslittle (of my money.) as possible.15
Linear programmingExample - diet s)Cost (serving)Brownie400322 2.50 / brownieChocolate icecream200224 1.00 / scoopCoke150041 1.50 / bottlePineapplecheesecake500045 4.00 / slice16
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceWhat are unknowns?––––x1 number of brownies to eat each dayx2 number of scoops of chocolate ice cream toeat each dayx3 number of bottles of Coke to drink each dayx4 number of pineapple cheesecake slices to eateach dayIn linear programming "unknowns" are calleddecision variables17
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceObjective is to minimize cost of food. Total daily cost isCost (Cost of brownies) (Cost of ice cream) (Cost of Coke) (Cost of cheesecake)– Cost of brownies (Cost/brownie) (brownies/day) 2.5x1– Cost of ice cream x2– Cost of Coke 1.5x3– Cost of cheesecake 4x418
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceTherefore, need to minimize2.5x1 x2 1.5x3 4 x419
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceConstraint 1 - calorie intake at least 500– Calories from brownies (calories/brownie)(brownies/day) 400x1– Calories from ice cream 200x2– Calories from Coke 150x3– Calories from cheesecake 500x4So constraint 1 is400 x1 200 x2 150 x3 500 x4 50020
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceConstraint 2 - chocolate intake at least 6 oz– Chocolate from brownies (Chocolate/brownie)(brownies/day) 3x1– Chocolate from ice cream 2x2– Chocolate from Coke 0x3 0– Chocolate from cheesecake 0x4 0So constraint 2 is3x1 2 x2 621
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceConstraint 3 - sugar intake at least 10 oz– Sugar from brownies (sugar/brownie)(brownies/day) 2x1– Sugar from ice cream 2x2– Sugar from Coke 4x3– Sugar from cheesecake 4x4So constraint 3 is2 x1 2 x2 4 x3 4 x4 1022
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceConstraint 4 - fat intake at least 8 oz– Fat from brownies (fat/brownie)(brownies/day) 2x1– Fat from ice cream 4x2– Fat from Coke 1x3– Fat from cheesecake 5x4So constraint 4 is2 x1 4 x2 x3 5x4 823
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceFinally, we assume that the amounts eaten arenon-negative, i.e., we ignore throwing up. Thismeans that we havex1 0, x2 0, x3 0, and x4 024
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / slicePutting it all together, we have to minimize 2.5x x 1.5x 4xsubject to the constraints400 x 200 x 150 x 500 x 5001x1 0andx2 0x3 0x4 012323443x1 2 x2 62 x1 2 x2 4 x3 4 x4 102 x1 4 x2 x3 5 x4 825
Linear programmingExample - diet problemFoodCaloriesChocolateSugar (ounces)Fat (ounces)Cost (serving)Brownie400322 2.50 / brownieChocolate ice cream200224 1.00 / scoopCoke150041 1.50 / bottlePineapple cheesecake500045 4.00 / sliceIn matrix notation, want tominimize f x subject to Ax b and x 0Twhere x1 400 200 150 500 500 2.5 x 3 6 1 2002 , b , x , and f A x3 2 10 1.5 244 x24158 4 4 26
Linear programmingMATLAB solves linear programming problem A x b minimize f T x such that Aeq x beq lb x ub where x, b, beq, lb, and ub are vectors and A and Aeqare matrices. Can use one or more of the constraints "lb" means "lower bound", "ub" means "upper bound"– Often have lb 0 and ub , i.e., no upper bound27
Linear programmingMATLAB linear programming solver islinprog(), which you can call various ways:x linprog(f,A,b)x linprog(f,A,b,Aeq,beq)x linprog(f,A,b,Aeq,beq,lb,ub)x linprog(f,A,b,Aeq,beq,lb,ub,x0)x linprog(f,A,b,Aeq,beq,lb,ub,x0,options)x linprog(problem)[x,fval] linprog(.)[x,fval,exitflag] linprog(.)[x,fval,exitflag,output] linprog(.)[x,fval,exitflag,output,lambda] linprog(.)28
Linear programmingExample - diet problemUs: minimize f T x subject to Ax b and 0 x x1 400 200 150 500 500 2.5 x 3 6 1 2002 , b , x , and f A x3 2 10 1.5 244 x24158 4 4 MATLAB: A x b minimize f T x such that Aeq x beq lb x ub Note two differences:29
Linear programmingExample - diet problemISSUE 1 - We have Ax b but need Ax bOne way to handle is to note thatif Ax b then -Ax -b, so can have MATLAB useconstraint (-A)x (-b)ISSUE 2 - We have 0 x but MATLAB wantslb x ub . Handle by omitting ub in call oflinprog(). If omitted, MATLAB assumes noupper bound30
Linear programmingExample - diet problemx linprog(f,A,b,Aeq,beq,lb,ub) We'll actually callx linprog(f,A,b,Aeq,beq,lb) If don't have equality constraints, pass []for Aeq and beq31
Linear programmingExample - diet problemFollow along now A -[ 400 200 150 500; 3 2 0 0; 2 2 4 4;.2 4 1 5 ]; b -[ 500 6 10 8 ]'; f [ 2.5 1 1.5 4]'; lb [ 0 0 0 0 ]'; x linprog( f, A, b, [], [], lb )Optimization terminated.x 0.0000 % brownies3.0000 % chocolate ice cream1.0000 % Coke320.0000 % cheesecake
Linear programmingExample - diet problemOptimal solution is x [ 0 3 1 0 ]T . In words,my son should eat 3 scoops of ice cream anddrink 1 Coke each day.33
Linear programmingExample - diet problemA constraint is binding if both sides of theconstraint inequality are equal when theoptimal solution is substituted.For x [ 0 3 1 0 ]T the set 400 x 200 x 150 x 500 x750 5003x 2 xbecomes 6 6 ,2x 2x 4x 4x110 1013 8214 50012 634 10322 x1 4 x2 x3 5 x4 8so the chocolate and sugar constraints arebinding. The other two are nonbinding34
Linear programmingExample - diet problemHow many calories, and how much chocolate,sugar and fat will he get each day? -A*xans ugarfatHow much money will this cost? f'*xans 4.5000 % dollars35
Linear programmingExample - diet problemBecause it's common to want to know the valueof the objective function at the optimum,linprog() can return that to you[x fval] linprog(f,A,b,Aeq,beq,lb,ub)where fval fTx [x fval] linprog( f, A, b, [], [], lb )x 0.00003.00001.00000.0000fval 4.500036
Linear programmingSpecial kinds of solutionsUsually a linear programming problem has a unique(single) optimal solution. However, there can also be:1. No feasible solutions2. An unbounded solution. There are solutions thatmake the objective function arbitrarily large (maxproblem) or arbitrarily small (min problem)3. An infinite number of optimal solutions. Thetechnique of goal programming is often used tochoose among alternative optimal solutions.(Won't consider this case more)37
Linear programmingCan tell about the solution MATLAB finds byusing third output variable:[x fval exitflag] .linprog(f,A,b,Aeq,beq,lb,ub)exitflag - integer identifying the reason the algorithmterminated. Values are10-2-3-4-5-7Function converged to a solution x.Number of iterations exceeded options.No feasible point was found.Problem is unbounded.NaN value was encountered during execution of the algorithm.Both primal and dual problems are infeasible.Search direction became too small. No further progress could be made.38
Linear programmingTry ItSolve the following problem and display theoptimal solution, the value of the objectivevalue there, and the exit flag from linprog()Maximize z 2x1 - x2 subject tox1 x2 12 x1 x2 6x1 , x2 039
Linear programmingTry ItFirst multiply second equation by -1 to getx1 x2 1 2 x1 x2 6x1 , x2 0Then, with objective function z 2x1 - x2rewrite in matrix form: x1 1 1 1 A , b , x , 2 1 6 x2 2 0 f and lb 1 0 40
Linear programmingTry It x1 1 1 1 2 0 A ,b ,x ,f andlb x 6 1 0 2 1 2 A [ 1 -1; -2 -1 ];b [ 1 -6 ]';f [ 2 -1 ]';lb [ 0 0 ]';41
Linear programmingTry ItIMPORTANT - linprog() tries tominimize the objective function. If youwant to maximize the objective function,pass -f and use -fval as themaximum value of the objective function42
Linear programmingTry It [x fval exitflag] linprog( -f, A, b, [],[], lb )Exiting: One or more of the residuals, duality gap,or total relative error has grown 100000 timesgreater than its minimum value so far: the dualappears to be infeasible (and the primal unbounded).(The primal residual TolFun 1.00e-008.)x 1.0e 061 *4.46494.4649fval -4.4649e 061 (-fval 4.4649e 061 !!!)exitflag -3 (Problem is unbounded)43
Linear programmingTry ItA farmer has 10 acres to plant in wheat and rye. Hehas to plant at least 7 acres. However, he has only 1200 to spend and each acre of wheat costs 200 toplant and each acre of rye costs 100 to plant.Moreover, the farmer has to get the planting done in12 hours and it takes an hour to plant an acre ofwheat and 2 hours to plant an acre of rye. If the profitis 500 per acre of wheat and 300 per acre of ryehow many acres of each should be planted tomaximize profits?44
Linear programmingTry ItDecision variables– x is number of acres of wheat to plant– y is number of acres of rye to plantConstraints "has 10 acres to plant in wheat and rye"– In math this is x y 10 " has to plant at least 7 acres"– In math this is x y 745
Linear programmingTry ItConstraints "he has only 1200 to spend and eachacre of wheat costs 200 to plant andeach acre of rye costs 100 to plant"– In math this is 200 x 100 y 120046
Linear programmingTry ItConstraints "the farmer has to get the planting done in12 hours and it takes an hour to plant anacre of wheat and 2 hours to plant an acreof rye "– In math this is 1x 2 y 1247
Linear programmingTry ItObjective function ". the profit is 500 per acre of wheat and 300 per acre of rye"– In math this is z 500 x 300 y48
Linear programmingTry ItPut it together– Constraints:x y 10x y 7200 x 100 y 1200x 2 y 12x 0y 0– Objective function:z 500 x 300 y49
Linear programmingTry ItRename x to x1 and y to x2Change x y 7 to -x - y -7 and then to-x1 - x2 -7x1 x2 10 x1 x2 7200 x1 100 x2 1200x1 2 x2 12z 500 x1 300 x2x1 0x2 050
Linear programmingTry ItWrite in matrix formMaximize z 500x 300x12x1 x2 10 x1 x2 7200 x1 100 x2 1200x1 2 x2 12x1 0x2 01 1 10 1 1 7 , b , x x1 , f 500 and lb 0 A x 300 0 200 100 1200 2 2 1 12 Maximizez f Tx51
Linear programming1 1 10 1 1 , b 7 , x x1 , f 500 and lb 0 A x 300 0 200 100 1200 2 1212 z f TxTry ItFind solution that maximizes profit.Display both A [ 1 1; -1 -1; 100 200; 2 1]; b [ 10 -7 1200 12 ]'; f [ 300 500 ]'; lb [ 0 0 ]'; [x fval] linprog( -f, A, b, [], [], lb ); x'ans 4.00004.0000 maxProfit -fvalmaxProfit 3.2000e 00352
Linear programmingTry It - blending problemAlloy Mixture Optimization (minimize expenses)There are four metals with the following properties:MetalDensity%Carbon%PhosphorPrice ( 1.5D59000.110.12.0We want to make an alloy with properties in the following 045Maximum60500.30.055What mixture of metals should we use to minimize the cost ofthe alloy?53
Linear programmingTry It - blending problemDecision variables– x1 is fraction of total alloy that is metal A– x2 is fraction of total alloy that is metal B– x3 is fraction of total alloy that is metal C– x4 is fraction of total alloy that is metal D54
Linear programmingMetalDensity%Carbon%PhosphorPrice ( mum59500.10.045Maximum60500.30.055Try It - blending problemDensity constraints Alloy density must be at least 5950–In math this is6500 x1 5800 x2 6200 x3 5900 x4 5950 Alloy density must be at most 6050–In math this is 6500x1 5800x2 6200x3 5900x4 605055
Linear programmingMetalDensity%Carbon%PhosphorPrice ( mum59500.10.045Maximum60500.30.055Try It - blending problemCarbon constraints Carbon concentration must be at least 0.1–In math this is0.2 x1 0.35x2 0.15x3 0.11x4 0.1 Carbon concentration must be at most 0.3–In math this is0.2 x1 0.35x2 0.15x3 0.11x4 0.356
Linear programmingMetalDensity%Carbon%PhosphorPrice ( mum59500.10.045Maximum60500.30.055Try It - blending problemPhosphor constraints Phosphor concentration must be at least 0.1–In math this is0.05x1 0.015x2 0.065x3 0.1x4 0.045 Phosphor concentration must be at most 0.3–In math this is0.05x1 0.015x2 0.065x3 0.1x4 0.05557
Linear programmingTry It - blending problemConstraintsSince only the four metals will make up thealloy, the sum of the fractional amountsmust be one: x1 x2 x3 x4 1Fractional parts must be non-negative:0 xifor i 1,2,3,4(Each part must also be 1, but that's handled by firstequation.)58
Linear programmingMetalDensity%Carbon%PhosphorPrice ( 1.5D59000.110.12.0Try It - blending problemObjective functionCost per kg z 2.0 x1 2.5x2 1.5x3 2.0 x459
Linear programmingTry It - blending problemPut it together 6500 x 5800 x 6200 x 5900 x 59501– Constraints:(Convert to )2346500 x1 5800 x2 6200 x3 5900 x4 6050 0.2 x1 0.35 x2 0.15 x3 0.11x4 0.10.2 x1 0.35 x2 0.15 x3 0.11x4 0.3 0.05 x1 0.015 x2 0.065 x3 0.1x4 0.0450.05 x1 0.015 x2 0.065 x3 0.1x4 0.055x1 x2 x3 x4 1xi 0, i 1,2,3,4–Objective function:z 2.0 x1 2.5x2 1.5x3 2.0 x460
Linear programmingTry It - blending problemWrite in matrix form 6500 5800 6200 5900 5950 6500 6050 580062005900 x1 x 0.2 0.35 0.15 0.11 0.1 2A , b , x x3 0.350.150.11 0.3 0.2 0.05 0.015 0.065 0.045 0.1 x4 0.0150.0650.1 0.05 0.055 6500 x1 5800 x2 6200 x3 5900 x4 59506500 x1 5800 x2 6200 x3 5900 x4 6050 0.2 x1 0.35 x2 0.15 x3 0.11x4 0.10.2 x1 0.35 x2 0.15 x3 0.11x4 0.3 0.05 x1 0.015 x2 0.065 x3 0.1x4 0.0450.05 x1 0.015 x2 0.065 x3 0.1x4 0.055x1 x2 x3 x4 1xi 0, i 1,2,3,4T 2.0 1 0 2.5 1 0 f , A EQ , b EQ 1, and lb 1.5 1 0 2.0 1 0 Minimizez f Tx61
Linearprogramming 6500 5800 6200 5900 5950 6500 6050 580062005900 x1 x 0.2 0.35 0.15 0.11 0.1 2 A ,b ,x x3 0.20.350.150.110.3 0.05 0.015 0.065 0.045 0.1 x4 0.0150.0650.1 0.05 0.055 T 2.0 1 0 2.5 1 0 f , A EQ , b EQ 1, and lb 1.5 1 0 2.0 1 0 Try It - blending problem A [-6500 -5800 -6200 -5900; 6500 5800 6200 5900;.-0.2 -0.35 -0.15 -0.11; 0.2 0.35 0.15 0.11;.-0.05 -0.015 -0.065 -0.1; 0.05 0.015 0.065 0.1 ]; b [ -5950 6050 -0.1 0.3 -0.045 0.055 ]'; f [ 2 2.5 1.5 2 ]'; Aeq [ 1 1 1 1 ]; beq 1; lb [ 0 0 0 0 ]';62
Linear programmingTry It - blending problem [x fval] linprog( f, A, b, Aeq, beq, lb )Optimization terminated.x 0.0000 - Metal A0.2845 - Metal B0.5948 - Metal C0.1207 - Metal Dfval 1.8448 - Profit in /kg63
MATLABLinearProgrammingQuestions?64
The End65
Linear programming MATLAB solves linear programming problem where x, b, beq, lb, and ub are vectors and A and Aeq are matrices. Can use one or more of the constraints "lb" means "lower bound", "ub" means "upper bound" – Often have lb 0 and ub , i.e., no upper bound minim