WIXLIB

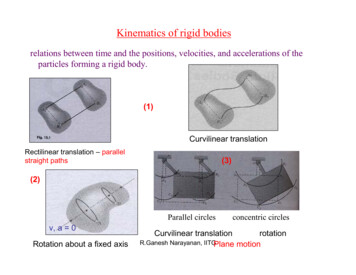
Kinematics of rigid bodiesrelations between time and the positions, velocities, and accelerations of theparticles forming a rigid body.(1)Curvilinear translationRectilinear translation – parallelstraight paths(3)(2)Parallel circlesv, a 0Rotation about a fixed axisconcentric circlesCurvilinear translationrotationR.Ganesh Narayanan, IITGPlane motion

(4)Sliding rodRolling wheelGeneral Plane motion – neitherrotation nor translation(5) Motion about a fixed pointR.Ganesh Narayanan, IITG

(1) TranslationConsider rigid body in translation:direction of any straight line inside the body is constant,all particles forming the body move in parallel lines.For any two particles in the body, rB rA rBADifferentiating with respect to time,rB rA rBA rAvB v ArB/A 0Magnitude constant since A,B belong to same rigid bodyAll particles have the same velocity.Differentiating with respect to time again,aB a AAll particles have the same acceleration.R.Ganesh Narayanan, IITG

vB v AaB a AWhen a rigid body is in translation, all the points of the bodyhave the same velocity and same acceleration at any given instantIn curvilinear translation, the velocity and acceleration change indirection and in magnitude at every instant; In rectilineartranslation, velocity, acceleration direction are same during entiremotionR.Ganesh Narayanan, IITG

(2) Rotation About a Fixed Axis: Velocity & AccelerationConsider rotation of rigid body about a fixedaxis AA’The length s of the arc described by P when thebody rotates through θ, s (BP ) θ (r sin φ ) θ θds lim (r sin φ ) rθ sin φv tdt t 0V dr ω rdtVector direction along the rotation axisAA’, angular velocity, ωk θ kR.Ganesh Narayanan, IITG

Differentiating to determine the acceleration,dv d (ω r )dt dtdωdr r ω dtdtdω r ω vdta Angular acceleration, αa α x r ω x (ω x ncomponentR.Ganesh Narayanan, IITG

Equations Defining the Rotation of a Rigid Body About a Fixed Axisω dθdtordt dθωd ω d 2θdωα 2 ωdtdθdtv dx/dta d2x/dt2a v (dv/dx)Uniform Rotation, α 0:θ θ0Equns. Can be used onlywhen α 0 & constant ωtUniformly Accelerated Rotation, α constant:ω ω0 αtθ θ 0 ω 0t ω21αt22 ω 02 2 α (θ θ 0x x0 vtv v0 atx x0 v0t ½ at2)R.Ganesh Narayanan, IITGv2 v02 2a (x-x0)

The rectangular block shown rotates about the diagonalOA with a constant angular velocity of 6.76 rad/s.Knowing that the rotation is counterclockwise as viewedfrom A, determine the velocity and acceleration of pointB at the instant shown.Angular velocity.Velocity of point B.vB ω x RB/O (i 6.24j 2.4 k) x (0.127i 0.396j) -0.95i 0.305j – 0.396 kAcceleration of point B.m/saB ω vB -3.2 i – 1.88j 6.23kR.Ganesh Narayanan, IITGm/s2

The assembly shown consists of two rods and arectangular plate BCDE which are welded together.The assembly rotates about the axis AB with a constantangular velocity of 10 rad/s. Knowing that the rotationis counterclockwise as viewed from B, determine thevelocity and acceleration of corner E.Find rB/A, rE/BFind angular velocity vector; ω ω (rB/A / lAB)1) vE ω x rE/B; 2) aE ω x vER.Ganesh Narayanan, IITG

Ring B has an inner radius r2 and hangs from thehorizontal shaft A as shown. Shaft A rotates with aconstant angular velocity of 25 rad/s and no slippingoccurs. Knowing that r1 1.27 cm, r2 6.35 cm, andr3 8.9 cm, determine (a) the angular velocity of ringB, (b) the acceleration of the points of shaft A and ringB which are in contact, (c) the magnitude of theacceleration of a point on the outside surface of ring B.R.Ganesh Narayanan, IITG

R.Ganesh Narayanan, IITG

(3) General Plane Motion General plane motion is neither a translation nor a rotation. General plane motion can be considered as the sum of atranslation and rotation. Displacement of particles A1 and B1 to A2 and B2can be divided into two parts:- translation to A2 and B1′- rotation of B1′ about A2 to B2R.Ganesh Narayanan, IITG

Absolute and Relative Velocity in Plane MotionAbsolute and Relative Velocity in Plane Motion Any plane motion can be replaced by a translation of an arbitrary referencepoint A and a simultaneous rotation about A.vB v A vBvBAA ω rBvBAv B v A ω rBA rωAR.Ganesh Narayanan, IITG

Point A as reference Assuming that the velocity vA of end A is known, wish to determine thevelocity vB of end B and the angular velocity ω in terms of vA, l, and θ. The direction of vB and vB/A are known. Complete the velocity diagram.vA cos θv B A lωvAv B v A tan θω cos θR.Ganesh Narayanan, lIITGvB tan θvAvA

Point B as reference Selecting point B as the reference point and solving for the velocity vA of end Aand the angular velocity ω leads to an equivalent velocity triangle. vA/B has the same magnitude but opposite sense of vB/A. The sense of therelative velocity is dependent on the choice of reference point. Angular velocity ω of the rod in its rotation about B is the same as its rotationabout A. Angular velocity is not dependent on the choice of reference point.R.Ganesh Narayanan, IITG

The crank AB has a constant clockwise angularvelocity of 2000 rpm.For the crank position indicated, determine (a) theangular velocity of the connecting rod BD, and (b)the velocity of the piston P.r The velocity vB is obtained from the crank rotation data.Crank ABω AB 2000 rev min 2π rad 209.4 rad s min 60 s rev vB ( AB )ω AB (3 in.)(209.4 rad s ) 628.3 in/sThe velocity direction is as shown.Connecting rod BD The direction of the absolute velocity vD is horizontal.The direction of the relative velocity vD B isperpendicular to BD. Compute the angle between thehorizontal and the connecting rod from the law of sines.sin 40 sin β 8 in.3 in.β 13.95 R.Ganesh Narayanan, IITG

vD BvD628.3 in. s sin 53.95 sin 50 sin76.05 vD 523.4 in. s 43.6 ft svDvDBBvP vD 43.6 ft s 495.9 in. s lω BDvD495.9 in. s8 in.l 62.0 rad sω BD B R.Ganesh Narayanan, IITGω BD (62.0 rad s )k

Instantaneous Center of Rotation in Plane Motion Plane motion of all particles in a slab can always bereplaced by the translation of an arbitrary point A and arotation about A with an angular velocity that isindependent of the choice of A. The same translational and rotational velocities at A areobtained by allowing the slab to rotate with the sameangular velocity about the point C on a perpendicular tothe velocity at A. The velocity of all other particles in the slab are the sameas originally defined since the angular velocity andtranslational velocity at A are equivalent. As far as the velocities are concerned, the slab seems torotate about the instantaneous center of rotation C.R.Ganesh Narayanan, IITG

How to obtain instantaneous center of rotationFig. 1Fig. 2 If the velocity at two points A and B are known, theinstantaneous center of rotation lies at the intersectionof the perpendiculars to the velocity vectors through Aand B . (fig. 1) If the velocity vectors at A and B are perpendicular tothe line AB, the instantaneous center of rotation lies atthe intersection of the line AB with the line joining theextremities of the velocity vectors at A and B. (fig. 2) If the velocity vectors are parallel, the instantaneouscenter of rotation is at infinity and the angular velocityis zero. (fig. 1) If the velocity magnitudes are equal, the instantaneouscenter of rotation is at infinity and the angular velocityis zero. (fig. 2)R.Ganesh Narayanan, IITG

Instantaneous center of a slab in plane motion can be located either on slab or onoutside the slab. If on the slab, the particle ‘C’ coinciding at the center of rotationhas zero velocity at that instant. This coincidence will not happen at another time.So velocity at time ‘t’ will not be same at t dt. The particle coinciding with the center of rotation changes with time and theacceleration of the particle at the instantaneous center of rotation ‘C’ is not zero. The acceleration of the particles in the slab cannot be determined as if the slabwere simply rotating about C. The trace of the locus of the center of rotation on the bodyis the body centrode and in space is the space centrode.R.Ganesh Narayanan, IITG

Same problemThe crank AB has a constant clockwise angularvelocity of 2000 rpm.For the crank position indicated, determine (a)the angular velocity of the connecting rod BD,and (b) the velocity of the piston P.vB 628.3 in/s; β 13.95 The instantaneous center of rotation is at theintersection of the perpendiculars to the velocitiesthrough B and D.γ B 40 β 53.95 γ D 90 β 76.05 BCCD8 in. sin 76.05 sin 53.95 sin50 BC 10.14 in. CD 8.44 in.R.Ganesh Narayanan, IITG

Determine the angular velocity about the center ofrotation based on the velocity at B.vB (BC )ω BDω BD vB 628.3 in. s BC 10.14 in.ω BD 62.0 rad s Calculate the velocity at D based on its rotation aboutthe instantaneous center of rotation.vD (CD )ω BD (8.44 in.)(62.0 rad s )vP vD 523 in. s 43.6 ft sR.Ganesh Narayanan, IITG

Absolute and Relative Acceleration in Plane Motion Absolute acceleration of a particle of the slab,aB a A aBAaB a A aB a A (a BA) (a B At)A nr Relative acceleration a B A associated with rotation about A includestangential and normal components,(a B A )t α rB A(a B A )n ω 2 rB A(a B A )t rα2(aR.Ganesh) rωB A n Narayanan, IITG

Rate of Change of vector with respect to a Rotating Frame Frame OXYZ is fixed. Frame Oxyz rotates about fixedaxis OA with angular velocity Ω Vector function Q(t ) variesin direction and magnitude.Rate of change of Q depends on frame of reference With respect to the rotating Oxyz frame, If Q were fixed within Oxyz then QisQ Qx i Q y j Qz kOXYZequivalent to velocity of a point in a rigid bodyQ Oxyz Q x i Q y j Qz kattached to Oxyz andQ x di/dt Q y dj/dt Q zdk/dt Ω Q With respect to the fixed OXYZ frame,()()(Q)OXYZ(Q) Q x i Q y j Qz k Qx di/dt Q y dj/dt Qz dk/dtOxyz Qx i Q y j Qz kRepresent velocity of particle, ΩxQR.Ganesh Narayanan, IITG

With respect to the fixed OXYZ frame,(Q)OXYZ() Q Oxyz Ω QThis relation is useful to find rate of change of Q w.r.t. fixedframe of reference OXYZ when Q is defined by its componentsalong the rotating frame OxyzR.Ganesh Narayanan, IITG

Coriolis Acceleration Frame OXYr is fixed and frame Oxy rotates with angularvelocity Ω . Position vector rP for the particle P is the same in bothframes but the rate of change depends on the choice offrame. The absolute velocity of the particle P is,v P (r )OXY Ω r (r )Oxy The absolute acceleration of the particle P is,ap vp Ωxr Ωxr d/dt [(r)Oxy]v P (r )OXY Ω r (r )Oxybut,r r rr&(r )OXY Ω r (r& )Oxy[]r rd r&r&&(r )Oxy (r )Oxy Ω (r& )Oxydtap Ω x r R.GaneshΩ x (ΩNarayanan,x r) 2IITGΩ x (r)Oxy (r)Oxy

ap Ω x r Ω x (Ω x r) 2Ω x (r)Oxy (r)Oxya α x r ω x (ω x r)Coriolisacceleration, acTwo vectors are normal to each other, 2ΩvOxyR.Ganesh Narayanan, IITG

Disk D of the Geneva mechanism rotates withconstant counterclockwise angular velocity ωD 10 rad/s.At the instant when φ 150o, determine (a) theangular velocity of disk S, and (b) the velocity ofpin P relative to disk S. From the law of cosines,r 2 R2 l 2 2Rl cos30 0.551R2From the law of sine,sinβ sin 30 sin 30 sin β Rr0.742r 37.1 mmβ 42.4 Magnitude and direction of absolute velocity of pin P arecalculated from radius and angular velocity of disk D.vP Rω D (50 mm )(10 radR.Ganeshs ) 500Narayanan,mm sIITG

The absolute velocity of the point P may be written asv P (r )OXY Ω r (r )OxyvP vP ′ vPsThe interior angle of the vector triangle isγ 90 42.4 30 17.6 vP′ vP sin γ (500 mm s )sin 17.6 151.2 mm s rω sωs 151.2 mm s37.1 mmωs 4.08 rad svP s vP cos γ (500 m s ) cos17.6 vP s (477 m s )42.4 Coriolis acceleration, ac 2 ωs vp/s 2 (4.08) (477) 3890 mm/s2R.Ganesh Narayanan, IITG

The crank AB has a constant clockwise angular velocity of 2000 rpm. For the crank position indicated, determine (a) the angular velocity of the connecting rod BD, and (b) the velocity of the piston P. The velocity is obtained from the crank rotavB tion data. r ( ) ( )3in.( )209 .4 rads 209 .4 rads rev 2 rad 60s min min rev 2000 B AB .