WIXLIB

A Circle Limit III Backbone Arc FormulaLuns Tee2Douglas Dunham121Marvell Semiconductor Inc.5488 Marvell LaneSanta Clara, CA 95054 USAgeom@luns.orgDepartment of Computer ScienceUniversity of Minnesota, DuluthDuluth, MN 55812-3036, USAddunham@d.umn.eduhttp://www.d.umn.edu/ ddunham/1

History - Outline Early 1958: H.S.M. Coxeter sends M.C. Escher a reprintcontaining a hyperbolic triangle tessellation. Later in 1958: Inspired by that tessellation, Escher creates Circle Limit I. Late 1959: Solving the “problems” of Circle Limit I,Escher creates Circle Limit III. 1979: In a Leonardo article, Coxeter uses hyperbolictrigonometry to calculate the “backbone arc” angle. 1996: In a Mathematical Intelligencer article, Coxeteruses Euclidean geometry to calculate the “backbonearc” angle. 2006: In a Bridges paper, D. Dunham introduces (p, q, r)“Circle Limit III” patterns and gives an “arc angle” formula for (p, 3, 3). 2007: In a Bridges paper, Dunham shows an “arc angle” calculation in the general case (p, q, r). Later 2007: L. Tee derives an “arc angle” formula inthe general case.2

The hyperbolic triangle pattern in Coxeter’s paper3

A Computer Rendition of Circle Limit IEscher: Shortcomings of Circle Limit I“There is no continuity, no ‘traffic flow’, no unity ofcolour in each row .”4

A Computer Rendition of Circle Limit III5

Poincaré Circle Model of Hyperbolic Geometry Points: points within the bounding circleLines: circular arcs perpendicular to the bounding circle (including diameters as a special case)6

The Regular Tessellations {m,n}There is a regular tessellation, {m,n} of the hyperbolicplane by regular m-sided polygons meeting n at a vertexprovided (m 2)(n 2) 4.The tessellation {8,3} superimposed on the Circle LimitIII pattern.7

Equidistant Curves and Petrie PolygonsGiven a hyperbolic line and a hyperbolic distance, thereare two equidistant curves, one on each side of the line,whose points are that distance from the given line.A Petrie polygon is a polygonal path of edges in a regular tessellation traversed by alternately taking the leftmost and right-most edge at each vertex.A Petrie polygon (blue) based on the {8,3} tessellation,and a hyperbolic line (green) with two associated equidistant curves (red).8

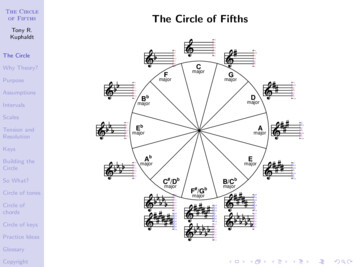
Coxeter’s Leonardo and IntelligencerArticlesIn Leonardo 12, (1979), pages 19–25, Coxeter used hyperbolic trigonometry to find the following expression forthe angle ω that the backbone arcs make with the bounding circle in Circle Limit III.cos(ω) (21/4 2 1/4)/2 or ω 79.97 Coxeter derived the same result, using elementary Euclidean geometry, in The Mathematical Intelligencer 18,No. 4 (1996), pages 42–46.9

Mathematical Intelligencer Cover10

Mathematical Intelligencer Contents Page11

“On The Cover:”Coxeter’s enthusiasm for the gift M.C. Escher gavehim, a print of Circle Limit III, is understandable.So is his continuing curiosity. See the articles onpp. 35–46. He has not, however said of what general theory this pattern is a special case. Not as yet.Annonymous Editor12

A General TheoryWe use the symbolism (p,q,r) to denote a pattern of fish inwhich p meet at right fin tips, q meet at left fin tips, and rfish meet at their noses. Of course p and q must be at leastthree, and r must be odd so that the fish swim head-to-tail(as they do in Circle Limit III).The Circle Limit III pattern would be labeled (4,3,3) inthis notation.13

A (5,3,3) Pattern14

Dunham’s Bridges 2006 PaperIn the Bridges 2006 Conference Proceedings, Dunhamfollowed Coxeter’s Leonardo article, using hyperbolic trigonometry to derive the more general formula that applied to(p,3,3) patterns:cos ω 12π1 3/4 cos2( 2p)sFor Circle Limit III, p 4 and cos ω agrees with Coxeter’s calculations.For the (5,3,3) pattern, cos ω ω 78.07 .15v uu 3 5 5t40v uu 3 2 4t8and, which

Dunham’s Bridges 2007 PaperIn the Bridges 2007 Conference Proceedings, Dunhampresented a 5-step process for calculating ω for a general(p, q, r) pattern. This calculation utilized the Weierstrassmodel of hyperbolic geometry and the geometry of a tessellation by “kites”, any one of which forms a fundamental region for the pattern.16

Weierstrass Model of Hyperbolic Geometry Points: points on the upper sheet of a hyperboloid oftwo sheets: x2 y 2 z 2 1, z 1.Lines: the intersection of a Euclidean plane throughthe origin with this upper sheet (and so is one branchof a hyperbola). ℓx A line can be represented by its pole, a 3-vector ℓy ℓzon the dual hyperboloid ℓ2x ℓ2y ℓ2z 1, so that theline is the set of points satisfying xℓx yℓy zℓz 0. 17

The Relation Between the ModelsThe models are related via stereographic projection from the Weierstrass model onto the (unit)Poincarédisk in the xy-plane toward the point 0 ,0 1 x/(1 z) x Given by the formula: y 7 y/(1 z) . z0 18

The Kite TessellationThe fundamental region for a (p, q, r) pattern can be takento be a kite — a quadrilateral with two opposite anglesequal. The angles are 2π/p, π/r, 2π/q, and π/r.19

A Nose-Centered Kite Tessellation20

The Geometry of the Kite TessellationℓOBPααωRQThe kite OP RQ, its bisecting line, ℓ, the backbone line(equidistant curve) through O and R, and radius OB.21

Outline of the Calculation1. Calculate the Weierstrass coordinates of the points Pand Q.2. Find the coordinates of ℓ from those of P and Q.3. Use the coordinates of ℓ to compute the matrix of thereflection across ℓ.4. Reflect the origin O across ℓ to obtain the Weierstrasscoordinates of R, and thus the Poincaré coordinates ofR.5. Since the backbone equidistant curve is symmetric aboutthe y-axis, the origin O and R determine that circle,from which it is easy to calculate ω, the angle of intersection of the backbone curve with the bounding circle.22

Details of the Central KiteℓPπpO π/2rRπ/2rπqQ23

1. The Weierstrass Coordinates of P and QFrom a standard trigonometric formula for hyperbolic triangles, the hyperbolic cosines of the hyperbolic lengths ofthe sides OP and OQ of the triangle OP Q are given by:cosh(dp) cos(π/q) cos(π/r) cos π/psin(π/q) sin(π/r)andcos(π/p) cos(π/r) cos π/qcosh(dq ) sin(π/p) sin(π/r)From these equations, we obtain the Weierstrass coordinates of P and Q: cos(π/2r)sinh(dq ) P sin(π/2r)sinh(dq ) cosh(dq ) cos(π/2r)sinh(dp) Q sin(π/2r)sinh(dp) cosh(dp) 24

2. The Coordinates of ℓThe coordinates of the pole of ℓ are given by ℓx P h Q ℓ ℓy P h Q ℓz Where the hyperbolic cross-product P h Q is given by: Py Qz Pz Qy Pz Qx PxQz P h Q PxQy Py Qx and where the hyperbolic norm of a pole vector V is givenby:s V Vx2 Vy2 Vz225

3. The Reflection Matrix - A Simple CaseThe pole corresponding to the hyperbolicline perpendic sinh d ular to the x-axis and through the point 0 is given coshd cosh d by 0 . sinh dThe matrix Ref representing reflection of Weierstrass pointsacross that line is given by: cosh 2d 0 sinh 2d 010 Ref sinh 2d 0 cosh 2dwhere d is the the hyperbolic distance from the line (orpoint) to the origin.26

3. The Reflection Matrix - The General CaseIn general, reflection across a line whose nearest point tothe origin is rotated by angle θ from the x-axis is givenby: Rot(θ)RefRot( θ) where,as usual, cos θ sin θ 0 sin θcos θ 0 .Rot(θ) 00 1From ℓ we identify sinh d as ℓz , and cosh d as (ℓ2x ℓ2y ),which we denote ρ. Then cos θ ℓρx and sin θ ℓρy .rFurther, sinh 2d 2 sinh d cosh d 2ρℓz and cosh 2d cosh2 d sinh2 d ρ2 ℓ2z .Thus Refℓ, the matrix for reflection across ℓ is given by: Ref ℓ ℓxρℓyρ0 ℓρyℓxρ 0 (ρ2 ℓ2z ) 0 2ρℓz 010 0 22 2ρℓz 0 (ρ ℓz )0 1 27ℓx ℓyρ ρℓy ℓx ρ ρ 0 0 0 0 1

4. The Coordinates of RWe use Refℓ to reflect the origin to R since the kite OP RQis symmetric across ℓ:R Ref ℓ 0 2ℓxℓz 0 2ℓy ℓz ρ2 ℓ2z1Then we project Weierstrass point R to the Poincaré model: u v 02ℓx ℓz1 ρ2 ℓ2z2ℓy ℓz1 ρ2 ℓ2z280

5. The Angle ω u u The three points v , v , and the origin determine the 00(equidistant curve) circle centered at w (u2 v 2)/2v onthe y-axis. The y-coordinate of the intersection points of this circle,x2 (y w)2 w 2, with the unit circle to beyint 1/2w v/(u2 v 2).In the figure showing the geometry of the kite tessellation,the point B denotes the right-hand intersection point.The central angle, α, made by the radius OB with the xaxis is the complement of ω (which can be seen since theequidistant circle is symmetric across the perpendicularbisector of OB).Thus yint sin(α) cos(ω), so thatcos(ω) yint v/(u2 v 2),the desired result.29

Luns Tee’s Formula for ωIn mid-2007, Luns Tee used hyperbolic trigonometry toderive a general formula for ω, generalizing the calculations of Coxeter in the Leonardo article and Dunham inthe 2006 Bridges paper.As in those previous calculations, Tee based his computations on a fin-centered version of the (p, q, r) tessellation,with the central p-fold fin point labeled P , the oppositeq-fold point labeled Q, and the nose point labeled R′.30

A Diagram for Tee’s FormulaωNRMPQLℓ bR′The right fin tip of a fish is at the origin, P ; its left fin tip isat Q; its nose is at R′, and its tail is at R. The “backbone”equidistant curve, b, goes through R and R′. The hyperbolic line ℓ through L, M and N has the same endpointsas b. The segments RN and P Q are perpendicular to thathyperbolic line.31

The GoalBy a well-known formula, the angle ω is given by:cos(ω) tanh(RN )Since RN M is a right triangle, by one of the formulas forhyperbolic right triangles, tanh(RN ) is related to tanh(RM )by:tanh(RN ) cos(6 N RM ) tanh(RM )But 6 LRM 6 P RQ π .rπ2 π2rsince the equidistant curve bisectsThusπππcos(6 N RM ) cos( ) sin( )2 2r2randπ) tanh(RM ) (1)2rso that our task is reduced to calculating tanh(RM ).tanh(RN ) sin(32

A Formula for tanh(RM )To calculate tanh(RM ), we note that as hyperbolic distances RP RM M P , so eliminating M P from this equation will relate RM toRP , for which there are formulas.By the subtraction formula for coshcosh(MP ) cosh(RP RM) cosh(RP ) cosh(RM) sinh(RP ) sinh(RM)Dividing through by cosh(RM ) gives:cosh(M P )/ cosh(RM ) cosh(RP ) sinh(RP ) tanh(RM )Also by a formula for hyperbolic right triangles applied to P M L andRM N :cosh(M P ) cot(6 P M L) cot( πq ) andπ)cosh(RM ) cot(6 RM N ) cot( π2 2rAs opposite angles, 6 P M L) 6 RM N , so dividing the first equationby the second gives another expression for cosh(M P )/ cosh(RM ):ππcosh(M P )/ cosh(RM ) cot( ) cot( )q2rEquating the two expressions for cosh(M P )/ cosh(RM ) gives:ππcosh(RP ) sinh(RP ) tanh(RM ) cot( ) cot( )q2rWhich can be solved for tanh(RM ) in terms of RQ:ππtanh(RM ) (cosh(RP ) cot( ) cot( ))/ sinh(RP ) (2)q2r33

The Final FormulaAnother formula for general hyperbolic triangles, appliedto QP R gives:πππππcosh(RP ) (cos( ) cos( ) cos( ))/ sin( ) sin( )prqprWe can calculate sinh(RQ) from this by the formula sinh2 cosh2 1.Plugging those values of cosh(RP ) and sinh(RP ) into equation (2), and inserting that result into equation (1) givesthe final result:cos(ω) πsin( 2r) (cos( πp ) cos( πq ))cos( πp )2 cos( πq )2 cos( πr )2 2 cos( πp ) cos( πq ) cos( πr ) 1)r34

Comments1. Substituting q r 3 into the formula and somemanipulation gives the same formula as in Dunham’s2006 Brigdes paper.2. Calculating cot(ω) gives the following alternative formula:πtan( 2r)(cos( πq ) cos( πp ))cot(ω) s(cos( πp ) cos( πq ))2 2 cos( πr ) 235

A (3,4,3) Pattern36

A (3,5,3) Pattern.37

A Nose-Centered (5,3,3) Pattern.38

Future Work Write software to automatically convert the motif of a(p,q,r) pattern to a (p’,q’,r’) motif. Investigate patterns in which one of q or r (or both) isinfinity. Also, extend the current program to draw suchpatterns. Find an algorithm for computing the minimum number of colors needed for a (p,q,r) pattern as in CircleLimit III: all fish along a backbone line are the samecolor, and adjacent fish are different colors (the “mapcoloring principle”).39

1996: In a Mathematical Intelligencer article, Coxeter uses Euclidean geometry to calculate the “backbone arc” angle. 2006: In a Bridges paper, D. Dunham introduces (p,q,r) “Circle Limit III” pa