Transcription
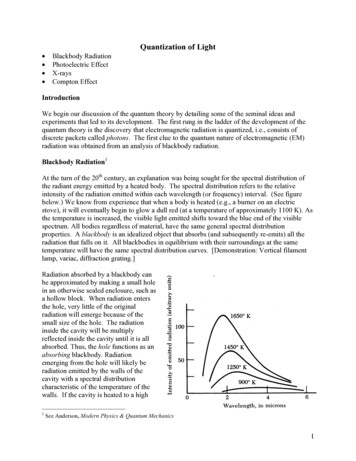
Quantization of LightBlackbody RadiationPhotoelectric EffectX-raysCompton EffectIntroductionWe begin our discussion of the quantum theory by detailing some of the seminal ideas andexperiments that led to its development. The first rung in the ladder of the development of thequantum theory is the discovery that electromagnetic radiation is quantized, i.e., consists ofdiscrete packets called photons. The first clue to the quantum nature of electromagnetic (EM)radiation was obtained from an analysis of blackbody radiation.Blackbody Radiation1At the turn of the 20th century, an explanation was being sought for the spectral distribution ofthe radiant energy emitted by a heated body. The spectral distribution refers to the relativeintensity of the radiation emitted within each wavelength (or frequency) interval. (See figurebelow.) We know from experience that when a body is heated (e.g., a burner on an electricstove), it will eventually begin to glow a dull red (at a temperature of approximately 1100 K). Asthe temperature is increased, the visible light emitted shifts toward the blue end of the visiblespectrum. All bodies regardless of material, have the same general spectral distributionproperties. A blackbody is an idealized object that absorbs (and subsequently re-emits) all theradiation that falls on it. All blackbodies in equilibrium with their surroundings at the sametemperature will have the same spectral distribution curves. [Demonstration: Vertical filamentlamp, variac, diffraction grating.]Radiation absorbed by a blackbody canbe approximated by making a small holein an otherwise sealed enclosure, such asa hollow block. When radiation entersthe hole, very little of the originalradiation will emerge because of thesmall size of the hole. The radiationinside the cavity will be multiplyreflected inside the cavity until it is allabsorbed. Thus, the hole functions as anabsorbing blackbody. Radiationemerging from the hole will likely beradiation emitted by the walls of thecavity with a spectral distributioncharacteristic of the temperature of thewalls. If the cavity is heated to a high1See Anderson, Modern Physics & Quantum Mechanics1
enough temperature, the hole will glow because of the visible radiation being emitted.Note that the wavelength at which the peak occurs shifts to higher values as the temperaturedecreases. An empirical relationship called Wien’s Displacement Law describes this shift:λ pT constant,(5.1)where T is the temperature in kelvins. In order to explain blackbody radiation spectra, Rayleighand Jeans regarded a blackbody as being composed of elementary oscillators that emit radiationof frequency equal to the oscillation frequency. All frequency modes are excited at alltemperatures. Each oscillator has an energy kT according to the classical equipartition theorem.Based upon this model, the following expression was obtained:8π kTρ (λ , T ) 4 ,(5.2)λwhere ρ (λ , T ) is the energy per unit volume per wavelength interval at equilibrium temperatureT. 2 Eq. (5.2) is the Rayleigh-Jeans law. While the R-J law gave a good description of theblackbody spectrum at large wavelengths, at small wavelengths ( λ 0 ), the energy densityρ . This calamitous result was known as the “ultraviolet catastrophe.”The shortcomings of the R-J theory stimulated Max Planck3 to take a fresh look at blackbodyradiation. Using statistical thermodynamics, Planck postulated that the total energy of theoscillators did not vary continuously. He divided the total energy into a finite number (integer) of“elements” of size ε . In addition, for his final expression for the energy density to fit the data,the energy element ε had to be proportional to the frequency of the radiation:(5.3)ε hf ,where h is a constant now called Planck’s constant.Planck’s final expression was 18π hc hc λ kTe 1) ,(5.4)5 (λwhich he used to fit the experimental blackbody data. He obtained excellent agreement using has a fitting parameter, with his best value for h being quite close to the presently accepted value h 6.626 10-34 J. s.ρ (λ , T ) Einstein later showed Planck’s result could only be derived if the energy of each oscillator isquantized in amounts of hf. Thus, the energy of each oscillator could only assume values thatwere integer multiples of hf:(5.5)ε n nhf , n 1, 2, 3,.[Mention cosmic microwave background (T 2.7 K). Departures from the blackbody spectrumgive information about the structure of the early universe.]Example - Show that Planck’s Law reduces to the R-J law for large λ .23Note: ( I , λ ) ( c / 4) ρ ( λ , T ) , where I is the radiated intensity.See: S. Brush, AJP 70, 119 (2002).2
Planck’s law: ρ (λ , T ) 18π hc hc λ kTe 1) .5 (λFor large λ , the exponent of e is small. Now, e x 1 x x2! x3! . For small x, i.e., x 1,23ex 1 x. Thus, e hc λ kT 1 hc λ kT .8π hc λ kT 8π kT .Hence, ρ (λ , T ) 5 λhcλ4Photoelectric EffectPlanck himself did not fully realize the implications of his quantum hypothesis. However,Einstein did, and used it to explain, in an exceedingly beautiful way, the theretofore puzzlingphenomenon called the photoelectric effect.The photoelectric effect is the emission of electrons from a material whose surface has beenirradiated by electromagnetic radiation. (In the most common cases, the material is a metal.) Itwas found that several aspects of the effect were inconsistent with the classical theory ofelectromagnetic waves. This represented another significant failure of classical theory. Thesalient characteristics of the photoelectric effect are given below:(1) Electrons are ejected immediately from the metal regardless of the intensity of the radiation.(2) The maximum kinetic energy (KE) of the ejected electrons is independent of the intensity.(3) The maximum KE of the ejected electrons increases with frequency.(4) Below a certain frequency, no electrons are ejected, regardless of intensity.(5) The number of electrons ejected increased with intensity of the radiation.Only item (5) could be explained satisfactorily by classical theory. Einstein departed fromclassical theory by extending Planck’s quantum hypothesis to the electromagnetic radiationitself. In other words, the radiation (light) itself is quantized in discrete packets called photons,which behave like particles with energy and momentum. Each photon has an energy E hf. Aphoton can collide with an electron near the surface of the metal. The photon gives up all itsenergy to the electron and ceases to exist. The electron, now endowed with extra kinetic energy,can overcome the energy barrier holding it inside the metal and escape from the metal. Thisinteraction is described very simply by the conservation of energy:hf φ K max ,(5.6)where φ is the work function of the metal, which is the minimum energy needed to eject anelectron, and Kmax is the maximum kinetic energy of the ejected electron. Einstein’s quantumtheory easily explained all the facets of the photoelectric effect. For example, the thresholdfrequency fo is that for which Kmax 0, i.e., hf 0 φ . If f fo, the photon will not have enoughenergy to remove an electron. Einstein’s theory was confirmed by an experiment conducted byMillikan (published in 1916).A schematic of the experimental apparatus is shown below. With a voltage applied as shown,electrons tend to be repelled from the plate. However, if they have sufficient KE, they canovercome the retarding potential and reach the plate. For a large enough retarding voltage, no3
electron will be able to reach the plate since all their KE will be converted to electrical PE beforereaching the plate. The current drops to zero at the stopping potential or stopping voltage Vs,given byeVs K max .(5.7)Thus,eVs hf φ ,(5.8)φ h Vs f .e e (5.9)or,By measuring the slope (h/e) Millikan confirmed that h had the same valued as found by Planck.Einstein was awarded the Nobel Prize in 1921 for his explanation of the photoelectric effect.[Show Millikan data, pp. 78 & 79, Rohlf.]Example: What is the maximum wavelength of photons capable of ejecting photoelectrons fromLi at u 0.95c? [ φ for Li 2.13 eV.] 1K (γ 1)mc 2 0.511 MeV 1.13 MeV. 1 (0.95)2 ()The maximum wavelength (minimum energy) required occurs when K K max . (Thus, the energyexpended by the electron to escape is equal to the minimum value, i.e., the work function.)hc φ K max 1.13 MeV. (φ is negligible.)λmaxNow, hc 1240 eV nm.1240 eV nmHence, λmax 1.1 10 3 nm.61.13 10 eV4
X-rays and the Compton Effect4Another mystery in the early days of modern physics was the fact that a monochromatic (singlewavelength) beam of x-rays that was scattered by a sample of material always contained a longerwavelength. Arthur Compton did careful experiments on x-ray scattering and showed that theappearance of the longer wavelength component could be explained by assuming the x-rays werequantized and that the x-ray photons interacted with electrons in the atoms of the material by“colliding” with them. Using conservation of momentum and energy, Compton obtained anexpression which described his experimental results beautifully. Before we analyze the ComptonEffect, we shall discuss some characteristics of x-rays.X-raysX rays are at the higher frequency (lower wavelength) electromagnetic spectrum. Frequencies ofx-rays are more than 1000 times those of visible light. Hence, X-ray photons are more than 1000times more energetic than visible photons. [Ex-ray 1-10 keV; Evisible l eV.]When electrons with kinetic energies in the keV range are used to bombard a heavy metal, theelectrons are decelerated very quickly and they radiate electromagnetic waves. The resultingspectrum of wavelengths is continuous and is called bremsstrahlung (“braking radiation”).Bremsstrahlung is characterized by a sharp cut-off at the low-wavelength end. This sharp cutoffis due to the fact that the maximum energy that an x-ray photon can have is all the kinetic energyof the bombarding electron. If the electrons are accelerated by a voltage V, then we havehc(5.10)eV hf cutoff .λcutoffThus,hc 1240 eV nm 1240λcutoff nm.(5.11)eVV (in eV)VNote that the ratio e/h can be ascertained from the slope of a fcutoff versus V plot.5Superimposed on the continuous spectrum are a few sharp, discrete peaks, which arecharacteristic of the target material. We shall see that these peaks are due to distinct energy-leveltransitions within atoms of the target material.X-ray DiffractionThe wavelength of x-rays are comparable to typical spacings between atoms in a crystallinematerial. Hence, crystalline materials can be used as a natural diffraction grating. Whenmonochromatic x-rays are scattered by a crystal, an analysis of the diffraction pattern givesvaluable information about the orientation of planes of atoms in the crystal and symmetries ofthose planes.6 Further, the distance between adjacent planes can be obtained.Show picture of Laue diffraction of ZnCoTe crystal]4May wish to cover Compton scattering first, so students can complete HW assignment.Bremsstrahlung is the inverse of the photoelectric effect: an electron transfers energy to an atom resulting in aphoton being emitted.6If x-rays directed along direction of symmetry, the diffraction pattern will have that symmetry.55
Consider x-rays incident on two adjacent atomic planes. (See figure below.) Bright spots will beseen in the diffraction pattern if there is constructive interference between the diffracted beams.For each atomic plane, the incident angle is equal to the angle of diffraction (this is why x-raydiffraction is sometimes called Bragg reflection after W.L. and W.H. Bragg, who did thepioneering work in x-ray diffraction). The condition for constructive interference between thetwo beams is:path difference nλ ,i.e.,2d sin θ nλ ,(Bragg equation)(5.12)where n is the order of the diffraction (usually n 1), θis the angle of diffraction, d is the distance betweenadjacent planes, and λ is the wavelength of the x-raybeam. Thus, if λ is known, d can be found.(Conversely, if d is known, λ can be found.) Theintensity of the diffraction spots depends on thearrangement of the atoms and the electron density. Ananalysis of intensity vs. θ gives important structuralinformation about the crystal. This is the field of x-raycrystallography.Compton Scattering7As mentioned previously, Compton scattering involves the scattering of x-rays by a sample ofmaterial in which the scattered beam contains a longer-wavelength component. Compton studiedthis phenomenon carefully using carbon. His analysis is based on the conservation of relativisticmomentum and energy in collision between an x-ray photon and a “free” electron at rest in the“laboratory” frame. The electron is really bound to an atom, but the energy of the x-ray photon isso much greater than the kinetic energy of the valence electron that the electron is effectively atrest. Based upon the photon picture, the scattered photon should have lower energy than theoriginal photon because the original photon gives up energy to the scattered electron. Since theenergy of the scattered photon is lower, it must have a smaller frequency and longer wavelengththan the original photon. Let us do this more quantitatively.Ei hcλiEf , pihcλf, pfθφE e, p e7Picture, p.73 Krane6
Conservation of momentum gives:Eq. (5.13) givespi p f cos θ pe cos φ .(5.13)0 p f sin θ pe sin φ .(5.14)pe cos φ pi p f cos θ ,(5.15)pe sin φ p f sin θ .(5.16)and Eq. (5.14) givesSquaring and adding Eqs. (5.15) and (5.16) givespe2 pi2 2 pi p f cos θ p 2f .(5.17)2Multiply Eq. (5.17) by c to obtainpe2 c 2 pi2 c 2 2 pi p f c 2 cos θ p 2f c 2 .(5.18)Now, from relativistic energy conservationEi me c 2 E f Ee ,(5.19)or,Ee Ei me c 2 E f .Squaring Eq. (5.20) givesEe (Ei me c 2 E f2(5.20)).2(5.21)ButEe2 pe2 c 2 me2 c 2 .Using Eqs. (5.18), (5.21), and (5.22), we find that(E m ci2e Ef) pc22 2i 2 pi p f c 2 cos θ p 2f c 2 me2 c 4 .(5.22)(5.23)After some algebra, one finds that8111 (1 cos θ ),E f Ei me c 2or, using E hc / λ , we obtainλ f λi h(1 cosθ ).me c(5.24)(5.25)h/mec is called the Compton wavelength of the electron.9 Note that the right hand sides of Eqs.(5.24) and (5.25) are always positive, which means that Ef is always less than Ei and8p i2 c 2 E i2 , p f2 c 2 E f2 , p ip fc 2 E iE f7
λ f λi always. Note also that the greatest change in λ occurs when cos θ 1, i.e., the photonis backscattered ( θ 180 ). In addition, note that the kinetic energy gained by the electron inthe scattering process is just given by Ke Ei – Ef.10 Finally, note that in the Compton spectra,there is always a spectral component at λ λi . This occurs because in some collisions of aphoton with an atom, the entire atom recoils, rather than a single electron being knocked out. Inthis case, the me in the Compton wavelength becomes matom, which is 104 times as large as me.Thus, λ f λi 0, i.e., λ f λi .Example: (p.72, Krane)X-rays of wavelength 0.2400 nm are Compton scattered and the scattered beam is observed at anangle of 60.0 relative to the incident beam. Find: (a) the wavelength of the scattered x-rays, (b)the energy of the scattered x-ray photons, (c) the kinetic energy of the scattered electrons, and (d)the direction of travel of the scattered electrons.Solution:(a) λ f can be found immediately from Equation (5.25):λ f λi h(1 cosθ )me c 0.2400 nm (0.00243 nm)(1 cos 60 ) 0.2412 nm.(b) The energy Ef can be found directly from λ f :Ef hc 1240 eV nm 5141 eV.λf0.2412 nm(c) Using the conservation of energy, we haveEi me c 2 E f Ee E f me c 2 K e .Thus,K e Ei E f .The initial photon energy Ei is hc / λi 5167 eV, and soKe 5167 eV - 5141 eV 26 eV.(d) Dividing Eq. (5.16) by Eq. (5.15) yieldstan φ 9p f sin θpi p f cos θ.-3h/mec 2.43 10 nm1022Ei mec Ef mec Ke8
Multiplying top and bottom by c, and recalling that E pc for photons, we haveE f sin θtan φ Ei E f cos θ(5141 eV)(sin 60 )(5167 eV) (5141 eV)(cos 60 ) 1.715. Thus,φ 59.7 .9
Quantization of Light Blackbody Radiation Photoelectric Effect X-rays Compton Effect . Einstein did, and used it to explain, in an exceedingly beautiful way, the theretofore puzzling . monochromatic x-rays are scattered by a crystal










