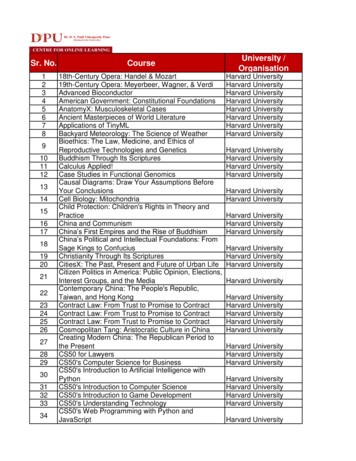
Transcription
Henry C. PinkhamLinear AlgebraJuly 10, 2015Springer
PrefaceThis is a textbook for a two-semester course on Linear Algebra. Although the prerequisites for this book are a semester of multivariable calculus, in reality everythingis developed from scratch and mathematical maturity is the real prerequisite. Traditionally linear algebra is the first course in the math curriculum where students areasked to understand proofs, and this book emphasizes this point: it gives the background to help students understand proofs and gives full proofs for all the theoremsin the book.Why write a textbook for a two semester course? First semester textbooks tendto focus exclusively on matrices and matrix manipulation, while second semestertextbooks tend to dismiss matrices as inferior tools. This segregation of matrix techniques on one hand, and linear transformations of the other tends to obscure theintimate relationship between the two.Students can enjoy the book without understanding all the proofs, as many numerically examples illustrate all the concepts.As is the case for most elementary textbooks on linear algebra, we only studyfinite dimensional vector spaces and restrict the scalars to real or complex numbers.We emphasize complex numbers and hermitian matrices, since the complex case isessential in understanding the real case. However, whenever possible, rather thanwriting one proof for the hermitian case that also works for the real symmetriccase, they are treated in separate sections, so the student who is mainly interestedin the real case, and knows little about complex numbers, can read on, skipping thesections devoted to the complex case.We spend more time that usual in studying systems of linear equations withoutusing the matrix technology. This allows for flexibility that one loses when usingmatrices. We take advantage of this work to study families of linear inequalities,which is useful for the optional chapter on convexity and optimization at the end ofthe book.In the second chapter, we study matrices and Gaussian elimination in the usualway, while comparing with elimination in systems of equations from the first chapter. We also spend more time than usual on matrix multiplication: the rest of thebook shows how essential it is to understanding linear algebra.v
viThen we study vector spaces and linear maps. We give the classical definitionof the rank of a matrix: the largest size of a non-singular square submatrix, as wellas the standard ones. We also prove other classic results on matrices that are oftenomitted in recent textbooks. We give a complete change of basis presentation inChapter 5.In a portion of the book that can be omitted on first reading, we study dualityand general bilinear forms. Then we study inner-product spaces: vector spaces witha positive definite scalar (or hermitian) product), in the usual way. We introduce theinner product late, because it is an additional piece of structure on a vector space.We replace it by duality in the early arguments where it can be used.Next we study linear operators on inner product space, a linear operator being alinear transformation from a vector space to itself, we study important special linearoperators: symmetric, hermitian, orthogonal and unitary operatrps, dealing with thereal and the complex operators separately Finally we define normal operators.Then with the goal of classifying linear operators we develop the important notion of polynomials of matrices. The elementary theory of polynomials in one variable, that most students will have already seen, is reviewed in an appendix. Thisleads us to the minimal polynomial of a linear operator, which allows us to establishthe Jordan normal form in both the complex and real case.Only then do we turn to determinants. This book shows how much of the elementary theory can be done without determinants, just using the rank and other similartools. Our presentation of determinants is built on permutations, and our definitionis the Leibnitz formula in terms of permutations. We then establish all the familiartheorems on determinants, but go a little further: we study the adjugate matrix andprove the classic Cauchy-Binet theorem.Next we study the characteristic polynomial of a linear operator, and prove theCayley-Hamilton theorem. We establish the classic meaning of all the coefficientsof the characteristic polynomial, not just the determinant and the trace.We conclude with the Spectral Theorem, the most important theorem of linearalgebra. We have a few things to say about the importance of the computations ofeigenvalues and eigenvectors. We derive all the classic tests for positive definite andpositive semidefinite matrices.Next there is an optional chapter on polytopes, polyhedra and convexity, a naturaloutgrowth of our study of inequalities in the first chapter. This only involves reallinear algebra.Finally, there is a chapter on the usefulness of linear algebra in the study ofdifference equations and linear ordinary differential equations. This only uses reallinear algebra.There are three appendices. the first is the summary of the notation used in theboof; the second gives some mathematical background that occasionally proves useful, especially the review of complex numbers. The last appendix on polynomials isvery important if you have not seen the material in it before. Extensive use of it ismade in the study of the minimal polynomial.LeitfadenThere are several pathways through the book.
vii1. Many readers with have seen the material of the first three sections of Chapter1; Chapters 2, 3, 4 and 5 form the core of the book and should be read carefully by everyone. I especially recommend a careful reading of the material onmatrix multiplication in Chapter 2, since many of the arguments later on dependessentially on a good knowledge of it.2. Chapter 6 on duality, and Chapter 7 on bilinear forms form an independent section that can be skipped in a one semester course.3. Chapter 8 studies what we call inner-product spaces: either real vector spaceswith a positive definite scalar product or complex vector spaces with a positivedefinite hermitian product. This begins our study of vector spaces equipped witha new bit of structure: an inner product. Chapter 9 studies operators on an inner product space. First it shows how to write all of them, and then it studiesthose that have a special structure with respect to the inner product. As alreadymentioned, the material for real vector spaces is presented independently for thereader who wants to focus on real vector spaces. These two chapter are essential.4. In Chapter 9, we go back to the study of vector spaces without an inner product. The goal is to understand all operators, so in fact logically this could comebefore the material on operators on inner product spaces. After an introductionof the goals of the chapter, the theory of polynomials of matrices is developed.My goal is to convince the reader that there is nothing difficult here. The keyresult is the existence of the minimal polynomial of an operator. Then we canprove the primary decomposition and the Jordan canonical form, which allow usto decompose any linear operator into smaller building blocks that are easy toanalyze.5. Finally we approach the second main objective of linear algebra: the study ofthe eigenvalues and eigenvectors of a linear operator. This is done in three steps.First the determinant in Chapter 11, then the characteristic polynomial in Chapter12, and finally the spectral theorem in Chapter 13. In the chapter concerning thespectral theorem we use the results on inner products and special operators ofchapters 8 and 9 for the first time. It is essential to get to this material in a onesemester course, which may require skipping items 2 and 4. Some applicationsshow the importance of eigenvector computation.6. Chapter 13 covers the method of least squares, one of the most important applications of linear algebra. This is optional for a one-semester course.7. Chapter 14, another optional chapter considers first an obvious generalization oflinear algebra: affine geometry. This is useful in developing the theory of iinearinequalities. From there is an a small step to get to the beautiful theory of convexity, with an emphasis on the complex bodies that come from linear inequalities:polyhedra and polytopes. This is ideal for the second semester of a linear algebracourse, or for a one-semester course that only studies real linear algebra.8. Finally the material on systems of differential equations forms a good applications for students who are familiar with multivariable calculus.9. There are three appendices: first a catalog of the notation system used, then a briefreview of some mathematics, including complex numbers, and what is most im-
viiiportant for us, the roots of polynomials with real or complex coefficients. Finallythe last appendix carefully reviews polynomials in one variable.Recommended BooksLike generations of writers of linear algebra textbooks before me, I must disclaimany originality in the establishment of the results of this book, most of which are atleast a century old. Here is a list of texts that I have found very helpful in writingthis book and that I recommend. On the matrix side, I recommend three books:Gantmacher’s classic two volume text [8], very thorough and perhaps somewhathard to read;Franklin’s concise and clear book [6].Denis Serre’s beautiful book [24], very concise and elegant.Horn and Johnson’s encyclopedic treatment of of matrices [13], which also showshow matrices and analysis can be interwoven. On the linear algebra side an excellent example of an older textbook is Minsky.More recently there is [12] - very complete. The classic textbook on the abstract side is Halmos’s book [10]. For those whowant to go even further in seeing how linear algebra is the first step in studying“abstract algebra”, Michael Artin’s text [1] is recommended, since he uses linearalgebra as the first building block to abstract algebra. Linear algebra is very useful in studying advanced geometry. An excellent bookthat quite unusually combines the linear algebra with the geometry is Shafarevich. Even more advanced is Manin’s book. There are two good self-described “second semester” linear algebra texts: SergeLang’s book [15] which suffers from its separation from his more elementary textthat develops the matrix techniques, and then Sheldon Axler’s beautifully writtenbook [2]. Finally there are books that focus on the computational side. It is because linearalgebra algorithms can be implemented on computers is a central reason that linear algebra has come to occupy a central position in the mathematics curriculum.We do not do much of that in this book. The classic text is Golub-Van Loan [9].There are books completely devoted to the computation of eigenvectors.Comments, corrections, and other suggestions for improving these notes are welcome. Please email them to me at hcp3@columbia.edu.H ENRY C. P INKHAMNew York, NYDraft of July 10, 2015
Contents1Linear Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.1 Linear Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.2 Geometry Interpretation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.3 Elimination . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.4 Examples of Elimination . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.5 Consequences of Linear Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.6 Diagonally Dominant Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.7 History . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1156101516172Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1 Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.2 Matrix Multiplication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.3 Square Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.4 Submatrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.5 Gaussian Elimination in Matrix Notation . . . . . . . . . . . . . . . . . . . . . . .2.6 Reduced Row–Echelon Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.7 Solving Linear Systems of Equations . . . . . . . . . . . . . . . . . . . . . . . . . .2.8 Elementary Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.9 Block Decomposition of Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.10 Column Operations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21212428323337384045493Vector Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.1 Scalars . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.2 Vector Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.3 Subspaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.4 Bases . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.5 Dimension . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3.6 Products and Direct Sums . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .51515255586163ix
xContents4Linear Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.1 Linear Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.2 The Nullspace and the Range of a Linear Map . . . . . . . . . . . . . . . . . .4.3 Composition of Linear Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.4 Linear Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.5 Invertible Linear Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4.6 Projections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5Representing Linear Maps by Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . 815.1 The Matrix of a Linear Map . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 815.2 The Linear Map of a Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 835.3 Change of Basis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 845.4 Equivalent Linear Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 875.5 Equivalent Linear Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 885.6 The Rank of a Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 905.7 More on Linear Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 935.8 Real and Complex Linear Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 955.9 Nilpotent Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 985.10 The Rank via Submatrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1016Duality . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1076.1 The Dual Space . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1076.2 Application: Lagrange Interpolation . . . . . . . . . . . . . . . . . . . . . . . . . . . 1096.3 Bilinear Forms: the General Case . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1126.4 Annihilators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1136.5 The Double Dual . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1156.6 Duality . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1177Bilinear Forms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1217.1 Bilinear Forms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1217.2 Quadratic Forms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1257.3 Decomposition of a Symmetric Bilinear Form . . . . . . . . . . . . . . . . . . . 1277.4 Diagonalization of Symmetric Bilinear Forms . . . . . . . . . . . . . . . . . . . 1297.5 Lagrange’s Diagonalization Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . 1307.6 Skew Symmetric Linear Forms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1327.7 Sylvesters Law of Inertia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1337.8 Hermitian Forms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1387.9 Diagonalization of Hermitian Forms . . . . . . . . . . . . . . . . . . . . . . . . . . . 1418Inner Product Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1438.1 Scalar Products . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1438.2 The Geometry of Euclidean Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1468.3 Gram-Schmidt Orthogonalization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1498.4 Orthogonal Projection in Euclidean Spaces . . . . . . . . . . . . . . . . . . . . . 1548.5 Solving the Inconsistent Inhomogeneous System . . . . . . . . . . . . . . . . 1568.6 Hermitian Products . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15965656872757677
Contentsxi8.78.8The Geometry of Hermitian Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . 160Scalar Product on Spaces of Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . 1629Operators on Inner Product Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1679.1 Adjoints on Real Spaces and Symmetric Matrices . . . . . . . . . . . . . . . 1679.2 Adjoints for Hermitian Products and Hermitian Matrices . . . . . . . . . . 1709.3 Positive Definite Operators and Matrices . . . . . . . . . . . . . . . . . . . . . . . 1739.4 Orthogonal Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1749.5 Unitary Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1769.6 Normal Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1779.7 The Four Subspaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17810The Minimal Polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18110.1 Linear Operators: the Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18110.2 Polynomials of Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18410.3 The Minimal Polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18610.4 Cyclic Vectors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18910.5 The Primary Decomposition Theorem . . . . . . . . . . . . . . . . . . . . . . . . . 19110.6 The Jordan Canonical Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19310.7 Uniqueness of the Jordan Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19510.8 The Jordan Form over the Real Numbers . . . . . . . . . . . . . . . . . . . . . . . 19710.9 An Application of the Jordan Canonical Form . . . . . . . . . . . . . . . . . . . 19711The Determinant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19911.1 Permutations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19911.2 Permutation Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20211.3 Permutations and the Determinant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20611.4 Properties of the Determinant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21011.5 The Laplace Expansion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21311.6 Cramer’s Rule . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21711.7 The Adjugate Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21811.8 The Cauchy-Binet Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21911.9 Gaussian Elimination via Determinants . . . . . . . . . . . . . . . . . . . . . . . . 22111.10Determinants and Volumes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22411.11The Birkhoff-Koenig Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22512The Characteristic Polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22712.1 The Characteristic Polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22712.2 The Multiplicity of Eigenvalues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23012.3 The Trace and the Determinant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23112.4 The Cayley-Hamilton Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23212.5 The Schur Unitary Triangularization Theorem . . . . . . . . . . . . . . . . . . 23312.6 The Characteristic Polynomial of the Companion Matrix . . . . . . . . . . 23512.7 The Minors of a Square Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23712.8 Computation of Eigenvectors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23812.9 The Big Picture . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 238
xiiContents12.10The Coefficients of the Characteristic Polynomial . . . . . . . . . . . . . . . 23813The Spectral Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24313.1 Triangulation of Complex Operators . . . . . . . . . . . . . . . . . . . . . . . . . . . 24313.2 The Rayleigh Quotient . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24413.3 The Spectral Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24613.4 The Spectral Theorem for Self-Adjoint Operators . . . . . . . . . . . . . . . . 24913.5 Positive Definite Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25013.6 The Spectral Theorem for Unitary Operators . . . . . . . . . . . . . . . . . . . . 25713.7 The Spectral Theorem for Orthogonal Operators . . . . . . . . . . . . . . . . . 25713.8 The Spectral Theorem for Normal Operators . . . . . . . . . . . . . . . . . . . . 25913.9 The Polar Decomposition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26113.10The Singular Value Decomposition . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26214The Method of Least Squares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26514.1 The Method of Least Squares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26514.2 Fitting to a Line . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26614.3 Connection to Statistics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26914.4 Orthogonal Least Squares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27314.5 Computational Techniques in Least Squares . . . . . . . . . . . . . . . . . . . . 27515Linear Inequalities and Polyhedra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27715.1 Affine Geometry . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27715.2 Systems of Linear Inequalities and Polyhedra . . . . . . . . . . . . . . . . . . . 28315.3 Convex Sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29015.4 Polyhedra and Polytopes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29715.5 Carathéodory’s Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30015.6 Minkowski’s Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30115.7 Polarity for Convex Sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30416Linear Differential Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30916.1 Differential Calculus Review . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30916.2 Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31016.3 The General Case . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31316.4 Systems of First Order Differential Equations . . . . . . . . . . . . . . . . . . . 31416.5 Eigenvector Computations for Linear ODE . . . . . . . . . . . . . . . . . . . . . 31516.6 Difference Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315ANotation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317A.1 Generalities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317A.2 Real and Complex Vector Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317A.3 Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318A.4 Linear Transformations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319
ContentsxiiiBMath Review . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321B.1 Sets and Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321B.2 Equivalence Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323B.3 Algorithms and Methods of Proof . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 324B.4 Dual Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 324B.5 Review of Complex Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325CPolynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327C.1 Polynomials: Definitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327C.2 The Euclidean Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329C.3 Roots of Polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330C.4 Great Common Divisors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332C.5 Unique Factorization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335C.6 The Fundamental Theorem of Algebra . . . . . . . . . . . . . . . . . . . . . . . . . 336DMatrices, Spreadsheets and Computer Systems . . . . . . . . . . . . . . . . . . . . 339D.1 Matrices and Spreadsheets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339D.1.1 Row Operations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 340D.1.2 Matrix Algebra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341D.2 Matrices in MatLab . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344D.2.1 Polynomials Passing Through Points . . . . . . . . . . . . . . . . . . . . 345D.2.2 Orthogonal Projections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347D.2.3 A Different Approximation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 349D.2.4 Comparison . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 353D.2.5 Exercise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 356D.2.6 Computing the Interpolation Polynomial . . . . . . . . . . . . . . . . . 356D.2.7 The kernel of the rectangular Vandermonde determinant . . . . 357References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359
Chapter 1Linear EquationsAbstract We define linear equations, both homogeneous and inhomogeneous, anddescribe what is certainly the oldest problem in linear algebra: finding the solutionsof a system of linear equations. In the case of three or fewer variables we explainhow elimination leads to the determinant - which we do not define in the generalcase. We do all this without introducing matrix notation. The sections 1.5 and 1.6are optional. The chapter concludes with a short section about the history of thesolution of linear equations1.1 Linear EquationsThe first problem of linear algebra is to solve a system of m linear equations in nunknowns x1 , x2 , . . . , xn . It was recognized early on that the case n m should beconsidered first. We will see why shortly.Many readers may already familiar with linear equations. Still, since it is centralto our concerns, here is the definition.Definition 1.1.1. A system of equations is linear if it can be writtena11 x1
linear algebra. Finally, there is a chapter on the usefulness of linear algebra in the study of difference equations and linear ordinary differential equations. This only uses real linear algebra. There are three append