Transcription
Algebra I, Algebra II, and TranscendentalsReview Department of Mathematical SciencesGeorge Mason UniversityRevised September 2017
ContentsIntroduction . 1Courses Requiring the Placement Test . 2Policies . 2Test Format . 3Learning Resources . 4Basic Algebra. 5Fractions . 6Decimal Notation . 7Percents . 8Ratios . . 10Algebraic Expressions . 11Linear Equations in One Variable . 11Linear Equations in Two Variables . 12Graph/Slope of a line . 13Algebra I . 14Linear Inequalities in 1 Variable . 14Absolute Value . 14Systems of Linear Equations . 15Linear Inequalities in 2 Variables . 16Multiplying Algebraic Expressions . 16Factoring Algebraic Expressions . 17Rational Expressions . 17More on Exponents . 18Radicals . 19Quadratic Equations . 19Functions Notation . 20Equations with Rational Expressions . 21Algebra II . 22More on Functions . 22Graphs of Functions. 24Transcendentals . 25Exponential Functions . 25Logarithmic Functions . 26Angle Measure . 26Right Triangle and Circular Functions Definitions . 27Graphs of Trigonometric Functions . 28Inverse Trigonometric Functions . 29Trigonometric Formulas and Identities . 30Answers . 31
Courses that Require the Placement TestThe Math Placement Test is given by the Department of Mathematical Sciencesto determine the readiness for the following courses: Math 104 Trigonometry and Transcendental Functions and Math 105Pre-CalculusMath 108 Introductory Calculus with Business ApplicationsMath 113 Analytic Geometry and Calculus IMath 123 Calculus Algebra/Trigonometry AMath 125 Discrete MathematicsCS 112 Computer Science IStudents should talk to an academic advisor to determine which Math course(s)they are required to take. All students admitted to the university are advised totake the Math Placement Test during the orientation process.PoliciesFor current policies and required minimum scores please visit thewebpage:http://math.gmu.edu/placement test.php1
Basic AlgebraBasic OperationsExample: John’s car insurance premium is 1515.00. He has the option ofmaking four equal payments but will be charged an additional 25 processingfee. If he chooses the four-payment option, what is the amount of each payment? 1515.00Solution: The processing fee is added to the premium 25.00 1540.00This amount is then divided by 43854 1540Each payment will be 385.00Exercise 1: A shipment of 1344 CD’s is to be packed into cartons containing 24CD’s each. How many cartons are necessary to ship these CD’s?Exercise 2: A loan of 10,020.00 is to be paid off in 60 equal monthly payments.How much is each payment (excluding interest)?Exercise 3: Susan’s Cell phone provider charges her 35.00 per month for thefirst 300 minutes of calls and 0.70 for each minute over 300. If she uses 340minutes of calls in a given month, how much will she be charged?2
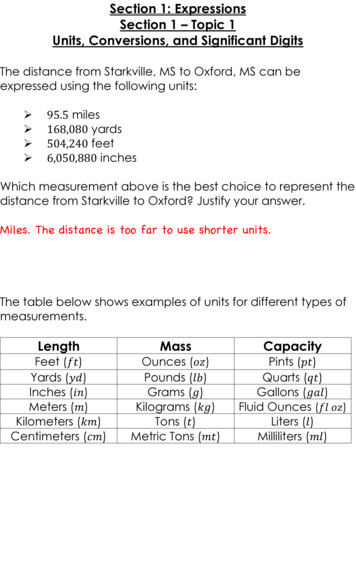
FractionsA fraction or rational number is of the form p where p and q are integers, andqq 0p is called the numerator and q is called the denominator. The fraction is said tobe reduced to lowest terms if p and q have no factors (other than 1) in common.The same number can be expressed as a fraction in many ways. These fractions1 , 3 , 5 , 10 , 124 12 20 40 48Only the first fraction is in reduced form.are called equivalent fractions: To change from a mixed number to an improper fraction, multiply the wholenumber by the denominator of the fraction and add the result to the numerator ofthe fraction. This gives the numerator of the improper fraction.Example:2 51 3 33 435 8 8( 5 1 3 2 )( 43 5 8 3 ) The product of two fractionsaca cis. That is, multiply numerators to bdb dget the numerator of the product and multiply denominators to get thedenominator of the product.Examples:2 4 8 11 9 996 2 6 2 12 5 1 5 5 The quotient of two fractionada ca d is equal to orcbb db cExample: 49 ounces of a solution is to be poured into test tubes with capacity13 ounces. How many test tubes will be filled?2Solution: 49 3172 49 49 1422714 test tubes will be filled.3
Exercise 4: Perform the indicated operation and give the result in reduced form.1 13a. b. 6c. 1 2 2 3d. 6 2 53 583 854a b a b c ccIf fractions do not have the same denominator then they must be changed to anequivalent form. The sum of two fractions with a common denominator isFind the sum 1 1 53 8Change each fraction to an equivalent form1 4 8 321 3 3 8 245 5 3 15 8 8 3 24Then add the equivalent fractions to get 1 1 5 32 15 47 or 1 233 8 24 24 2424Example:Exercise 5:form14a. 6 Perform the indicated operation and give the result in reduced78b. 7 310 4c.5 1 8 6d. 21 7 4 12Decimal NotationRational numbers or fractions can also be expressed in decimal notation.13 can be written as 7.137100.125 is equivalent to1125or81000 When adding or subtracting numbers in decimal notation, make sure to alignthe decimal point.4
Example:Find the sum 23.1 3.7823.1Solution: 3.7826.88 When multiplying two numbers in decimal notation, first multiply thenumbers disregarding the decimal point(s). Next put the decimal point in theproduct. The number of places to the right of the decimal point in the productshould be the SUM of the places to the right of the decimal point in each of thefactors.Example:Solution:Find the product6.35 2.1635 216351270013335The product should have three places to the right of the decimal point.The result will be 13.335Example: Carlos is getting paid 10.80 per hour for the first 40 hours he isworking and one time and a half that wage for each extra hour. If he works 43.5hours this week, how much will he earn?Solution:Carlos is paid 10.80 1.5 16.20 per hour of overtimeHe will earn: (40 10.80) (3.5 16.20) 488.70PercentsThe symbol% is used to indicate the fraction 1 or the ratio: 1 to 1001002323% is equivalent toor .23100100100% is equivalent toor 1.001005
Exercise 6: Change the decimal to percenta. .25b. .085c. 1.52Exercise 7: Change the percent to a decimala. 2%b. 5 1 %c. 0.3%2Example: A class contains 12 female and 8 male students. What percent of theclass is female?Solution:There are a total of 20 students in the class.12 out of 20 or 12 are female2012 60 60% of the class is female20 100Exercise 8: Find the followinga. 30% of 75b. 4% of 196c. 120% of 300Example: Suppose 60% of a class is female. Of these females, 20% arefreshman. What percent of the class is female upper class students?Solution: If 20% of the females are freshman, then 80% of females are upperclass students.80% of 60% .80 .60 .48so 48% of the class are female upper class studentsExample: Suppose we know that 40% of a class or 16 students are male. Howmany students are in the class?Solution:We knowThat isSo40% of (the number) is 16.40 the number 16 the number 16 40 students.40Example: Before graduating, Joe worked in a convenience store and earned 5.85/hr. He started a new job that is paying him 18.95/hr. What is thepercent increase in his hourly rate?actual increaseSolution: % increase so 18.95 5.85 or 224% after5.85originalrounding.6
RatioThe ratio of two numbers a and b is written a to b, a:b orabWe can think of this as a fraction in order to simplify it.The ratio 10:5 is equivalent to 2:1.32.5 32.5 2 65 52 10The ratio 32.5 to 5 is equivalent to 65 to 10 since 5 To show two ratios are equal use the following:A C if and only if AD BC BDExample: Show that 12.5 : 5 is equivalent to the ratio 5:2Solution: Since12.5 2 25 5 5 , 12.5 5 i.e. 12.5: 5 is52equivalent to the ratio 5:2.Example: How much water should be mixed with 7 cups of salt to make a12% saline solution?7 12 x 100Solution: We have the proportionMultiply to get1312 x 7001x 583So we need 58 7 51 part total 1cups of water.3Exponents When working with algebraic expressions involving exponents, the followingproperties of exponents are used:1.x a x b x a bxaa b2. b xx3. x a b x ab4. xy a xa yaa x xa5. ay y 6.x 0 1 for any x 07
Exercise 9: Simplify each of the following expressions using the rules ofexponents a. 3x 42b.Exercise 10: Find the product4a 102ab 5c. 5x 3 y 7 z 0 12 xy 6 z 2 16 x 5 y 2 5 x 2 2 xy 2 3Algebraic ExpressionsMost of Algebra involves manipulating expressions that contain variables.Example: Evaluate the expression using the indicated value of the variable 3k 1 k 5 Solution:for k 2 3 2 1 2 5 6 1 2 5 7 3 substitute -2 in the expression for k-21Exercise 11: Evaluate the expression using the indicated value of the variablea. 2 x 6 x 3 for x 221x for x 4b. 4 x 1 5 Exercise 12: Combine the terms below and simplify the result.a. 4 x 3 8x 2b. 16a 2b 4 a 3b c.4 x 3x 1 510Linear Equations in One VariableA linear equation in one variable can have a unique solution, no solution orinfinitely many solutions. When it has no solution, the equation is calledinconsistent.Example: Solve the following equations by isolating the variable.2 x 15 4 x 21Solution:2x 15 4x 4x 21 4x6 x 15 216 x 15 15 21 15Add 4x to both sidesAdd 15 to both sides8
6 x 36 1 1 6 x 36 6 6 x 6Example: Solve the equationSolution:Multiply both sides by 16The equation has a unique solution16 x 4 4 x 3 16 x 16 x 1216x 16x 16x 12 16x0 12Example: Solve the equationSolution:Distribute the 4Add -16x to both sidesThe equation is inconsistent.10 x 3 x 5 2 6 x 10 x 510x 3x 15 12x 20 x 5Clear the parentheses bydistributingCombine like terms13x 15 13x 150 0Since the last statement is always true, every real number will be asolution.Linear Equations in Two VariablesA solution for an equation in two variables is a replacement for each of thevariables so that when substituted, the resulting statement is true. We generallywrite the solution as an ordered pair. For example, 2, 5 is a solution of theequation 3x y 11 . When the variable x is replaced by 2 in the equation andthe variable y is replaced by 5, the resulting statement is true. The linearequation in two variables has an infinite number of solutions. The graph of thesesolutions is a line in the x-y plane.Example: The formula in two variables gives the conversion betweenFahrenheit and Celsius temperatures. x C to y F 9x 325Find the temperature in degrees Celsius that corresponds to 212 F9Solution:Substitute the value 212 for y212 x 325y 9
180 9x5100 xAdd -32 to both sidesMultiply both sides by 59A solution of the equation is 100, 212 The Graph of a LineWe can graph the solutions of any linear equation on a set of axes called theEuclidean Plane. In the case of the linear equation, the solutions form a line.\Wecan measure how much and in which direction the line tips using the slope.The slope-intercept form of the equation is : y mx bIf the equation is in this form, the line has slope m and y-intercept (0, b)The y-intercept is the point where the line intersects the y-axis.Example: In the graph below, find the x and y intercepts and the slope.Solution:x intercept: (-12, 0)y intercept: (0, 6)Slope is 1/2Example: Find the slope and y-intercept of the line with equation:5x 10 y 25Solution: Write the equation in slope-intercept form: y 1 x 5221 and the y-intercept 5 The slope is 0, 22 Parallel lines have identical slopes. Lines are perpendicular if their slopes have1the relationship m1 m2Example: Find the slope of a line that is perpendicular to the line5x 10 y 25Solution: The line5x 10 y 25 has slope 1 .2Any line perpendicular to it will have slope m - 2.10
Algebra IThe Algebra I section of the test measures your ability to perform basicalgebraic operations and to solve problems that involve algebraic concepts.Only those students attempting to place into Math 108, Math 112, Math 125,Math 113, CS 112 will be given questions from the Algebra I section. Inaddition to all material in the Basic Algebra, the following exercises andexamples provide a refresher of the material that is tested in the Algebra Isection.Linear Inequalities in One VariableUnlike linear equations, linear inequalities have an infinite number of solutions.We can use a number line or interval notation to indicate the solutions. Any realnumber can be added to or subtracted from both sides of the inequality. We canmultiply or divide both sides by any nonzero real number but, if we multiply ordivide by a negative number, the inequality sign must be reversed.-9Example: Solve the inequality3 x 25Subtract 2 from both sides: 1 -9 x5-5Multiply both sides by -5/9:³x9The solution is the interval:]Absolute Value Equations and InequalitiesThe absolute value of a number is defined to be its distance from 0 on thenumber line. x for x 0x x for x 0Example: Solve the equation for x 15 3x 75Solution:15 3x 75 orx 20 or15 3x 75x 30Example: Solve the inequality 2 x 5 15Solution:2 x 5 15 or 2 x 5 15x 10 orx 511
Distance Formula The distance between two points x1 , y1 and x2 , y2 is given bythe formula:d x2 x1 2 y2 y1 2The formula uses the Pythagorean TheoremExercise 1: Find the distance between the points 2, 5 and 1, 8 Systems of Linear EquationsWe sometimes group equations together and investigate whether they have acommon solution. This is called a system of equations. The system of linearequations has a solution if there is an ordered pair x, y that satisfies eachequation in the system. A system of linear equations can have exactly onesolution, no solution or infinitely many solutions. There are several methodsavailable to solve systems of linear equations. The next example illustrates theElimination Method. 3x 2 y 48 9 x 8 y 24Example: Solve the system Solution:3x 2 y 48 multiply by -3: 9 x 6 y 1449 x 8 y 249 x 8 y 24 14 y 168y 12Add:Solve for y:The value 12 is substituted for y in either of the original equations.3x 2 12 48 Solve the resulting equation for x3x 24 483x 24x 8The solution to the system is (8, 12)Exercise 2: Solve the systems 3x y 5 5 x 2 y 10a. 3x y 2 6 x 2 y 10b. 12
Linear Inequalities in Two VariablesLinear inequalities in two variables can be solved by graphing. The solution isan infinite set of ordered pairs in the plane. We can indicate the solution byshading the region that contains these ordered pairs.Example: Solve the inequality 5y ³ 3x -15Solution: Graph the line that results from replacing the inequality sign with anequal sign. Here, graph the line 5y 3x -15 This line partitions the plane intothree sets:The solutions of 5y 3x -15 5y 3x -155y 3x -15In the inequality, test an ordered pair from the plane that does not lie on the line.Using (0,0), we get: 5(0) ³ 3(0) -15 which is a true statement.Shade the half-plane of points that satisfy the inequality. See the graph below.In a similar way we can solve a system of inequalities. The graph below showsì5y ³ 3x -15ïthe solutions to the system í y 0ïx ³ 0îMultiplying Algebraic ExpressionsWe use the Distributive Law to multiply algebraic expressions.Example: Find the product 6 x 2 x 10 Solution:6 x 2 x 10 6 x 2 x 6 x 10 12 x 2 60 x13
To multiply 2 binomial factors, we apply the Distributive Law twice andcombine like terms. x 7 2 x 1 x 7 2x 1 x 2x 1 7 2x 1 Example: Find the productSolution: x 2 x x 1 7 2 x 7 1 2 x 2 x 14 x 7 2 x 2 13x 7The result of this multiplication is called a quadratic expression. We “undo” themultiplication in a process called factoring.Factoring Algebraic ExpressionsThe next two examples show the factoring process. In the first, we factor out thehighest common factor among the terms. In the second, we write the quadraticexpression as a product of 2 binomial factors.Example: Factor the expression 16 x 2 24 xSolution:16 x 2 24 x x 16 x 24 8 x 2 x 3 The terms have the factorx in commonThey also have a factor of8 in commonExample: Factor the expression t 2 18t 40Solution:t 2 18t 40 t 20 t 2 Special Factorings:a 2 b 2 (a b)(a b)a 3 b 3 (a b)(a 2 ab b 2 )a 3 b 3 (a b)(a 2 ab b 2 )Rational ExpressionsRational expressions are fractions where the numerator and/or denominatorinvolve variables. We can reduce, add, subtract, multiply and divide theserational expressions using the rules of fractions. You may want to review therules of fractions in the Basic Algebra section on page 6.14
35 7 xx 3x 10Example: Reduce the rational expression2Solution: In order to reduce the expression we must factor both the numeratorand the denominator, then cancel any factors common to both.35 7 x7 5 x x 3x 10 x 2 x 5 7 x 5 x 2 x 5 7 x 2 2Example: Find the sumFactor the numeratorCancel the common factor4x 3 x 1 x2 9 x 3Solution:4x 3 x 1 x 3 x 1 Use a common denominator4x 3 2x 9 x 3 x 3 x 3 x 3 x 3 4x 3 x 2 4x 3 x 3 x 3 x2x2 95x21a bSolution: Using the rules of dividing fractions we get:a b5x2 5 x 2 a b 1Example: Simplify the expressionMore Exponents The definition of exponents is extended to include all rational numbers:x aab1 axx b xaExercise 3: If x 2 find the value of x-33Exercise 4: Find the value of2327 91215
RadicalsWhen simplifying algebraic expressions involving radicals, the followingproperties of radicals are used:1.2.3.nnmx n y n xyx ynxnyxn wherey 0 x mn Example: Find the product 6 5 1 5 Solution: 6 5 1 5 6 1 6 5 1 5 5 5 1 5 528 3 7Exercise 5: Find the sum:Exercise 6: Simplify each of the following expressionsa.8a 6 b 5b.28u 7 v 37uv 2Exercise 7: Rationalize the denominator to simplify:c.38 x 5 y 152 23 2Quadratic EquationsAn equation of the form ax bx c 0 is called a quadratic equation. Theequation will have two, one or no real number solutions. There are severalmethods available to find the solutions of a quadratic equation. The followingexamples illustrate these methods.2Example: Solve the equation 2 x 2 20Solution:2 x 2 20x 2 10x 10Isolate the term involving the radicalTake the square root of both side of the equation16
Example: Solve the equation x 2 4 x 4 25Solution:x 2 4 x 4 25x 2 4 x 21 0bring all terms to one sidefactor the left side x 7 x 3 0x 7 0 or x 3 0x 7 orExample: Solve the equationx 39x 2 6x 1 0Solution: In the quadratic formula: x a 9 , b 6 and c 1x set each factor equal to zerothe equation has 2 solutions b b 2 4acwe use2a 6 6 2 4 9 1 6 2 918sinceb 2 4ac 0we get only one solution x 1 to the equation.3 The expression b 2 4ac is called the discriminant. It tells us how manysolutions a quadratic equation will have.If b 2 4ac 0 the equation has 2 real number solutionIf b 2 4ac 0 the equation has 1 real number solutionIf b 2 4ac 0 the equation has no real number solutionExercise 8: Solve the equationsa. 4 x 2 49 02x 2 9x 5 02c. x 4 x 6 0b.Function NotationFunctions can be defined using a list of ordered pairs, a graph, a table, or anequation.The following equation defines a function: f x x 2 1 .Each value of x is paired with the value f x .f 3 32 1 8 so the pair 3, 8 is in the function f.f 10 10 2 1 99 so the pair 10, 99 is in the function f.2f 10 10 1 99 so the pair 10, 99 is in the function f.17
Example: For the function f x f 2 Solution:x2 1find f 2 and f b 1 x 3( 2) 2 1 3 3 2 3 1f b 1 (b 1) 2 1 b 2 2b (b 1) 3b 4Complex Rational ExpressionA complex rational expression is one in which a rational expression appears inthe numerator and/or denominator. Simplifying the complex rational expressionis equivalent to finding the quotient of the expression in the numerator with theexpression in the denominator.1xyExample: Simplify the complex rational expression1 1 x ySolution: Combine the terms in the denominator first.1 1 y x x yxyNext, find the quotient of the numerator with the denominator1 y x 1xy xyxyxy y x 1y xEquations with Rational ExpressionsGiven an equation involving rational expressions we can find an equivalentequation with no rational expressions. To find the equivalent equation wemultiply the entire equation by the least common denominator (LCD). Aftersolving the equivalent equation, we must check the solution in the original to seeif it makes any denominator equal to zero. If so, we discard that solution.Example: Solve the equationSolution:1 1 3 x 5 2xThe LCD of the rational expressions is 10x10 x 113 10 x 10 x x52xMultiply equation by 10x18
10 2 x 15 2x 5x 52Example: Solve the equationSolution:Solve the resulting equation4 1 x3x 3The LCD of the rational expressions is 3x3x 41 3x 3x x Multiply equation by 3x3x34 x 3x 2 Solve the resulting equationUse the quadratic formula3x 2 x 4 0x 1 12 4 3 ( 4)2 3x 1 492 3x 1 and Exercise 9: Solve the equation4322x 36x 5 2x 3 x 1x 2x 3Algebra IIThe Algebra II section of the test measures your ability to solve problems thatinvolve more advanced Algebra than the previous section. Only those studentsattempting to place into Math 113 and CS 112 will be given questions from theAlgebra II section. The following exercises and examples provide a refresher ofmaterial that is tested in the Algebra II section.More on FunctionsA function is a set of ordered pairs where each first component is paired withexactly one second component. The set of first components is called the domainand the set of second components is called the range.Unless otherwise stated, the domain of the function f x x 2 1 , is all realnumbers. Any real number a can be paired with another real number using theequation f x x 2 1 . The pair can be written a, a 2 1 . 19
Suppose we have the function g t 3 . We say g t is undefined at t 0t3since the expressionis undefined. On the other hand, g t is defined at any0real number other than 0. The domain of g t is all real numbers except t 0 .Suppose we have the function f x x 5 . In order for the expressionx 5 to represent a real number, the expression x 5 must not be negative.For this function the domain is all real numbers x 5 . The average rate of change for a function f(x) is the change in f(x) over thechange in x.average rate of change f ( x ) xAlternatively, it is the slope of the secant line passing through the two points(x1, f(x1)) and (x2, f(x2))Exercise 1: Let f x 1; Find each of the following:2x 6a. the domain of f x b. the range of f(x)c. the average rate of change from x -1 to x 5Exercise 2: Let g x 13 x; Find each of the following:a. the domain of g x b. the range of g(x)c. the average rate of change from x -2 to x 2 We can compose two functions by applying one right after the other.Example: For the functions f and g defined in the exercises 1 and 2, finda. f g 6 b. g f 2 311Solution: f g 6 f f 3 ( 6) 3 20 1 1 g 1 or2 ( 2) 6 2 5/ 2g f 2 g 25Example: The function values of f and g are given in the table below. Use themto finda. f g 0 b. g f 3 20
x0123f(x)-30-21g(x)3210Solution: a. f g 0 f 3 1b. g f 3 g 1 2 Some functions have an inverse. The inverse of a function will interchangethe real numbers in the ordered pair. If a, b is in the function f then b, a is inf 1 , the inverse of f . Keep in mind, that not all functions have inverses.x 5The functions f x 3x 5 and f 1 x are inverses.3Notice f contains the pair (3,14) and f-1 contains the pair (14, 3). This is truefor all ordered pairs of the function f.Graphs of FunctionsWe can graph the set of ordered pairs of a function on a set of axes just as wedo with linear equations in 2 variables.The graph of a quadratic function f ( x) ax 2 bx c is a parabola.The vertex of the parabola is located at b , f ( b ) 2a 2aThis point on the graph is either a minimum or a maximum for the function. Theleading coefficient a, determines which. For a 0, the function takes on a b maximum at x and the range of the function is y y f b .2a 2a bFor a 0, the function takes on a minimum at x and the range of the2a function will be y y f b . 2a Example: In the graph of f ( x ) x 2 4 x 7 below, find the x and yintercepts and the vertex.21
Solution:y intercept: (0, 7)x intercept: nonevertex: (2, 3)note: (2, 3) is the minimum of f(x) To graph the function y c f ( x a ) b we shift the graph of f(x)right a units (for a 0), left a units for a 0)up b units for b 0, down b units for b 0vertically stretch the graph of f(x) by a factor of c, c 1vertically shrink the graph of f(x) by a factor of c, for 0 c 1Example: The graph above can be viewed as a shift of y x(2 units right and 3 units up). The function can be written in the form:2f ( x) ( x 2) 2 3TranscendentalsThe test measures your ability to work with exponential, logarithmic andtrigonometric functions of the right triangle and the unit circle. The graphs ofthese functions and some common trigonometric formulas are given in the nextfew pages.Exponential FunctionsAn exponential function is one in which the variable occurs in the exponent.The base determines whether the function is increasing or decreasing.f ( x) a x for a 1Domain: all real numbersRange: y 0f ( x) a x for a 1Domain: all real numbersRange: y 022
Logarithmic FunctionsA logarithmic function is the inverse of an exponential function.This is the natural logfunction, (the inverse ofy ex)f(x) ln xDomain: x 0Range: all real numbersExample: Evaluate: a. log 2 8Solution:a.b. log 5 1log 2 8 3 since 23 8c. log10 .001b. log 5 1 0 since50 1c. log10 .001 3 since 10 3 .001x 3Example: Solve the equation for x: e 10Solution: Isolate x by taking the log of both sides. Here use ln the natural log.ln e x 3 ln 10x 3 ln 10x 3 ln 10 .6974Example: Solve the equation for x: log 4 ( x 13) 6Solution: Use the inverse function to isolate x4 log4 ( x 13) 4 6x 13 4 6x 4083Angle MeasureAn angle can be measured in degrees or in radians. A full revolution is 360 or2 radians. We use this information to convert from one measure to the other.The following proportion shows the relationship between x degrees and yradians.x 360 y 2 Example: Find the degree measure of an angle whose radian measure is 2 3Solution:x360 2 / 3 2 2 x 360 2 / 3 so x 12023
Right Triangle Definitionsopphypadjcos hypopptan adjsin hypopphypsec adjadjcot oppcsc Definitions of Circular FunctionsSpecial AnglesDegreeRadian0300π/645π/460π/390π/2sin θ0cos θ11/ 22/23/23/23 /32/211/ 21tan θ003--csc θ-2sec θ12 3/3cot θ--3212 3/323 /31--02Sum and Difference Formulassin u v sin u cos v cos u sin v cos u v cos u cos v sin u sin v 24
Graphs of the Trigonometric Functionsf(x) sin(x) period: f(x) cos(x) period: f(x) tan(x)period: Exercise 1: Find the period ofa.sin 2 x b. x cos 4 c. x tan 3 Exercise 2: Which has the shortest period?a.y cos x b. y 1cos x2c.1y cos(2 x) d. y cos x225
Inverse Trigonometric FunctionsThe inverse sine function, wr
2 u 5 12 5 2 1 6 5 2 6u u The quotient of two fraction d c b a y is equal to c d b a u or cb ad Example: 49 ounces of a solution is to be poured into test tubes with capacity 2 1 3 ounces. How many test tubes will be filled? Solution: 14 7 2 49 2 7 49 2 1