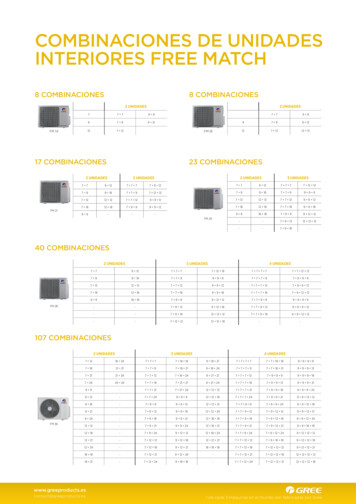
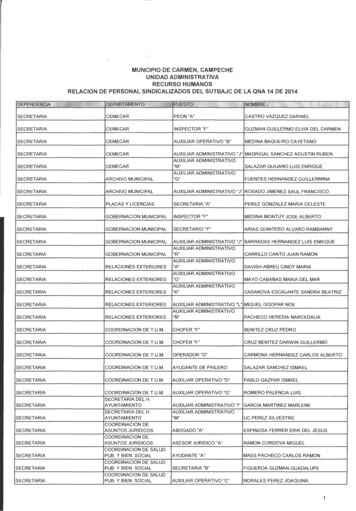
Transcription
Procesos Químicos IIUNIDAD Nº4Métodos matemáticos de optimización no restringidaBúsqueda unidimensionalMuchos métodos de optimización de problemas con restricciones (univariables y multivariables)involucran la resolución de un problema de optimización en una dimensión.Los métodos analíticos imponen demasiadas restricciones a las funciones objetivos. Además, nosiempre es posible resolver el sistema de ecuaciones analíticamente. Por este motivo sedesarrollaron los métodos numéricos.Existen dos tipos de métodos numéricos, a saber: Métodos directos: sólo utilizan los valores de las función objetivo. Métodos indirectos: utilizan las condiciones necesarias, las derivadas (analíticas onuméricas) y la función objetivo.Los métodos indirectos requieren el cálculo de las derivadas primeras y segundas. Sin embargo,muchas veces obtener las derivadas es una tarea difícil, y hasta es posible que ni siquiera seconozca la forma analítica de la función objetivo. Esto plantea la necesidad de contar conmétodos capaces de trabajar únicamente con los valores (experimentos) de la función objetivo.Estos son los métodos de búsqueda directa.La obtención de un valor de la función objetivo significará en algunos casos evaluar un modelomatemático, mientras que en otros significará realizar un experimento. Sea como sea, siempreserá conveniente llegar al óptimo realizando la menor cantidad de evaluaciones. Esa es la misiónde los métodos de búsqueda directa, a partir de los resultados de las evaluaciones realizadas,sugerirán el siguiente experimento de forma tal de aumentar la velocidad de convergencia. Esdecir, que estos métodos diseñarán un adecuado plan de experiencias.El plan de experiencias puede ser secuencial o simultáneo. Cuando disponemos de un equipo porun tiempo limitado, puede ser que nos veamos obligados a realizar una serie de experimentossimultáneos. Estos experimentos son independientes, los experimentos realizados no influyensobre la forma de realizar el siguiente. Un mejor enfoque es el plan de experiencias secuencial.Este método analiza los resultados obtenidos en un experimento para sugerir la forma de realizarel próximo.Los métodos indirectos tienen una ventaja inherente: la convergencia es normalmente rápida,pero no son buenos para funciones no lineales multivariables, estos métodos dan como resultadoun punto que puede encontrarse muy cercano al valor óptimo buscado. Los métodos directostienen la ventaja de que pueden más fácilmente tratar problemas que involucran funciones condiscontinuidades, puntos de inflexión y puntos finales, pero necesitan la definición de un criteriode precisión, estos métodos dan como solución al problema de optimización un intervalo dondepuede encontrarse el valor óptimo.Métodos numéricos para optimización de funciones de una variablePara la aplicación de estos métodos es necesario conocer el intervalo inicial 0 donde estacontenido el óptimo de la función objetivo, y asegurar la unimodalidad de la función en elintervalo en estudio.Un método de optimización para una función de una sola variable podría ser determinar unagrilla (tan fina como se quiera) de valores de x y calcular los valores de f(x) en cada valor de lagrilla, el óptimo sería el mejor valor de f(x). Si utilizamos este procedimiento para funcionesmultimodales, el tiempo de cálculo se vuelve prohibitivo. La selección del método de búsqueda1
Procesos Químicos IIdel óptimo es una solución de compromiso entre la complejidad del procedimiento y el númerode evaluaciones necesarias.1. Métodos indirectos: Newton, Quasi-Newton y SecanteEs de suponer que si además de unimodalidad y continuidad en las funciones que queremosoptimizar, se requiere también la derivabilidad de las mismas, podremos incrementar laeficiencia de los algoritmos de búsqueda.Nos referiremos en esta sección a métodos de búsqueda de óptimos en funciones derivables.Recordemos en primer lugar que la condición necesaria para que un punto x* sea óptimolocal de una función derivable es que se anule su derivada en ese punto, f (x*) 0. Cuandof(x) es una función de tercer grado o superior, la solución analítica de la ecuación f (x) 0 secomplica. Por tanto, requerimos un método de búsqueda que se aproxime sucesivamente alpunto estacionario de f(x).La efectividad de estas técnicas se evalúa mediante la velocidad de convergencia quepresentan. Convergencia linealx k 1 x * c0 c 1 convergencia lentaxk x * Convergencia de orden px k 1 x * cc 0,pxk x *p 1 convergencia muy rápidaSi p 2 la convergencia se dice que es cuadrática Convergencia superlinealx k 1 x * 0limxk x *k convergencia rápidaMétodo de NewtonEl método de Newton requiere que la función sea dos veces derivable. Se expresa como:x k 1 x k ( )( )f ' xkf '' xkasegurando que para cada paso k, f(xk 1) f(xk), para la búsqueda de un mínimo.Este método utiliza la condición de que f’(x) 0. Ventajas: es un proceso que converge cuadráticamente en forma local. Para unafunción cuadrática converge con solo una iteración. Desventajas: se deben calcular las derivadas primeras y segundas, si las derivadassegundas son nulas el método converge lentamente, si existen más de un extremo elmétodo puede no converger en el valor deseado.2
Procesos Químicos IIDesafortunadamente el método depende de la elección del punto de partida y de la naturalezade la función. Es bastante posible que este método no converja hacia el verdadero puntoestacionario. La figura siguiente ilustra esta dificultad. Si comenzamos en un punto a laderecha de x0, las aproximaciones sucesivas se alejarán del punto estacionario x*.Método de Quasi-NewtonEste método es una solución a las limitaciones del método de Newton. En el caso en que lafunción objetivo no sea conocida o no puedan evaluarse las derivadas, estas puedenreemplazarse por aproximaciones de diferencias finitas:[ f (x h ) f (x h )]xk 1 x k2h[ f (x h ) 2 f (x ) f (x h )]h2La desventaja adicional de este método consiste en la necesidad de evaluar funcionesadicionales en cada iteración, también es necesario conocer el valor de h (paso de ladiferencia finita).Método de la SecanteEl método de la secante combina el método de Newton con un esquema de reducción deintervalo para encontrar, si existe, la raíz de la ecuación f (x) 0, en el intervalo (a,b).En este método la condición necesaria se resuelve mediante la siguiente expresión:3
Procesos Químicos II( )()f ′ xk m x xk 0donde m es la pendiente de la recta que une los puntos xp y xq, dada por:f ′ xq f ′ x pm xq x pEste método aproxima la derivada de la función a una línea recta, m aproxima la segundaderivada de la función.( )x* x q [ f ′(x )q( )( )( )](xf ′ xq f ′ xpq xp)donde x * es la aproximación a x* en la iteración nº k.Este método comienza utilizando dos puntos xp y xq, la elección de estos puntos debe hacersede tal manera que los valores de las derivadas sean de signos opuestos. Este método es deconvergencia más lenta que el método de Newton.2. Métodos directos: eliminación de regionesEste tipo de métodos se centra en la búsqueda de las soluciones óptimas mediante sucesivasreducciones del intervalo de estudio y en la eliminación de subintervalos.Si la función es unimodal, se puede definir un criterio para eliminar regiones donde seguro elóptimo no se encuentra. Para ello necesitamos evaluar la función en dos puntos y aplicar algode lógica. En la figura siguiente se indica cual sería la región eliminada para los tres casosposibles en la búsqueda de un máximo.4
Procesos Químicos IIEs fundamental el hecho de que la función estudiada sea unimodal, al menos dentro deldominio de interés. La utilidad de esta propiedad radica en el hecho de que si f(x) esunimodal, entonces solamente es necesario comparar f(x) en dos puntos diferentes parapredecir en cuál de los subintervalos definidos por esos puntos no se va a encontrar elóptimo.Cuando el subintervalo “sobreviviente” tenga una longitud suficientemente pequeña, labúsqueda termina. La gran ventaja de estos métodos de búsqueda es que solamente requierenevaluaciones de la función y no necesitamos ninguna hipótesis adicional acerca de laderivabilidad de la misma.Búsqueda a intervalos igualesEste método de búsqueda reduce en 1/3 la longitud del intervalo en cada iteración. Entoncessi L0 es la longitud original del intervalo (b-a) y Lk es la longitud luego de k iteraciones:k 2 L L0 3 kMétodo de la bisección o dicotomíaEste método elimina exactamente la mitad del intervalo en cada paso. En este caso los puntosde búsqueda x1 y x2 se encuentran más próximos entre sí, manteniendo la equidistancia conlos bordes.k 1 L L0 2 kMétodo de FibonacciCon este método se conoce ya el rango inicial de búsqueda y en cada evaluación el métodotiende a acorralar el punto óptimo.El intervalo inicial de es L0 y se define 1 como el siguiente incremento:F 1 L0 n 2Fndonde n, es el número de iteraciones que se desea realizar (en función a la tolerancia de errorque se desea) y Fn es el número de Fibonacci para n evaluaciones, y se define así: F0 F1 1,Fn Fn-1 Fn-2, n 2,3,. , la secuencia de Fibonacci es entonces 1,1,2,3,5,8,13,21,34,55 Se tiene entonces x1 1 y x2 L0 - 1Se supone que se quiere minimizar a la función unimodal f(x). Entonces si f ( x1 ) f (x 2 ) ,rechazamos el intervalo 0 x x1 y si f ( x1 ) f (x 2 ) , rechazamos el intervalo x2 x1 L0.5
Procesos Químicos IIGráficamente se tiene que, si originalmente la función es como la que se ilustra en la figura,en la segunda iteración se rechaza el intervalo 0 x x1. En forma gráfica tenemos:A continuación se calcula el siguiente incremento 2 y se define x3 como L0- 2F 2 L1 n 3L1 L0 x1Fn 1En caso de que se hubiera rechazado el intervalo x2 x1 L0, entonces L1 x2 y x3 2. Se tieneen la segunda evaluación lo siguiente: si f ( x 2 ) f (x3 ) , rechazamos el intervalo x1 x x3 o sif ( x 2 ) f (x3 ) , rechazamos el intervalo x2 x L0.El proceso se repite hasta llegar al número n de iteraciones prefijadas. La efectividad en estecaso, 1/Fn, mide la tolerancia del error en el entorno del punto óptimo. Así, por ejemplo, si sedesea un error menor al 1%, se necesitan 11 evaluaciones de este método, puesto queF11 144 y 1/F11 1/144 0.01 1%.Método de la Sección AureaEn la sección Aurea se ubican dos puntos interiores de manera tal que el intervalo eliminadoen cada iteración sea de la misma proporción que el intervalo total. Solo un nuevo punto debeser calculado en cada iteración.Consideremos la localización simétrica de dos puntos como en la figura:Partimos de un intervalo [0, 1] de longitud unidad (simplemente por conveniencia) ylocalizamos dos puntos, cada uno a una fracción τ de cada extremo. Con esta simetría,independientemente de qué valor de la función sea el más pequeño, la longitud del intervaloque permanece es siempre τ. Supongamos que eliminamos el subintervalo de la derecha.6
Procesos Químicos IISe puede observar a partir de la figura que el punto que queda, de los dos anteriores, estásituado a una distancia 1 τ de uno de los extremos.En la estrategia que se plantea el método del número de oro el punto que permanece en elinterior del nuevo intervalo está ubicado en la posición relativa en la que se encontraba elotro punto, que ahora limita la zona, la distancia 1 τ debe corresponder a una fracción τ delintervalo (que es de longitud τ). Con esta elección de τ, el siguiente punto debe localizarse auna fracción τ de la longitud del intervalo desde el extremo de la parte derecha.1 τ τ τ1Por tanto, con la elección de τ que satisfaga 1 τ τ2, el patrón de búsqueda permanece en elintervalo reducido de la siguiente figura.La solución de esta ecuación cuadrática es τ 1 5, siendo la solución positiva de la2misma τ 0.61803 . . .El subintervalo final luego de cada iteración es:Lk (0.618)k 1L0Método de Fibonacci y aproximación al método de la Sección AureaPara determinar la ubicación de los puntos según el método de Fibonacci se utiliza, comoFvimos, la expresión 1 L0 n 2 . La relación de números de Fibonacci para grandes valoresFnde n se acerca a 0.3820, como se observa en la siguiente tabla:nFn 2Fn345671/3 0.33332/5 0.40003/8 0.37505/13 0.38468/21 0.38108913/34 21/55 0.3823 0.3818Entonces para valores de n grandes, el enésimo número de la seria de Fibonacci puedecalcularse con la siguiente relación:1(1.6180)n 1Fn57
Procesos Químicos IIEsto indica que en el método de Fibonacci para n grandes, la búsqueda debe comenzarseutilizando la relación 1 0.3820 L0 .La aproximación al valor óptimo obtenida luego de n experimentos será entonces:LL LLα N N N 4 L 2 (0.6180 )n 1L1 L N 1 L N 2L1Como podemos observar esta relación es la utilizada en el método del número de oro,k 1Lk (0.618) L0 . Entonces el método de la serie de Fibonacci, para más de cuatroiteraciones se convierte en el método del número de la Sección Aurea.Métodos de búsqueda preplaneadaEste método realiza todos los experimentos a la vez, determinando luego el intervalo quecontiene el óptimo.2.1. Comparación de los métodos de eliminación de regionesComparemos ahora las eficiencias relativas de los métodos de eliminación de regiones quehemos visto. Denotemos el intervalo de incertidumbre original como L0 y al intervalo deincertidumbre final, después de N evaluaciones de la función objetivo le llamaremos LNSupongamos ahora que consideramos a la reducción fraccional (RF) del intervalo originalcomo una medida de mérito de los métodos de eliminación de regiones.Tenemos entonces:k 2 L L0 3 Búsqueda a intervalos igualeskkMétodo de la bisección o dicotomíaMétodo de FibonacciMétodo de la Sección Áurea 1 L L0 2 2 0 LLk FN 1 kLk (0.618)k 1L0Las reducciones fraccionales pueden obtenerse fácilmente:Búsqueda a intervalos igualesLk 2 L0 3 kkMétodo de la bisección o dicotomíaMétodo de FibonacciMétodo de la Sección Áurea8Lk 1 L0 2 Lk 2 L0 FN 1 Lkk 1 (0.618)0L
Procesos Químicos IILa siguiente tabla muestra los valores de RF(N) para distintos valores de N. Estos valoresson indicativos de la eficiencia de cada método.N 5N 10N 15Búsqueda a intervalos iguales0,1320,0170,002Método de la bisección o dicotomía0,9130,9880,998Método de Fibonacci0,1540,0140,0013Método de la Sección Áurea0,1460,0130,0012De esta tabla se desprende que los métodos más eficientes son el de Fibonacci y la seccióndorada. En la práctica, suele calcularse el número de iteraciones que se requieren paraobtener una precisión dada. Esto se puede obtener usando LN ε, siendo ε la precisiónrequerida.3. Métodos de aproximación polinomialOtra clase de métodos de minimización unidimensional, localizan un punto x cercano alóptimo mediante interpolación y extrapolación utilizando polinomios como modelos de lafunción.La idea básica de los métodos de aproximación polinomial es que si la función essuficientemente “suave”, entonces puede ser aproximada mediante un polinomio, y dichopolinomio puede entonces usarse para predecir la ubicación del óptimo. Para que estaestrategia sea efectiva, es necesario que la función a optimizar sea tanto unimodal comocontinua.Interpolación cuadráticaLa interpolación cuadrática aprovecha la ventaja de que un polinomio de segundo grado confrecuencia proporciona una buena aproximación de la forma de la función en las cercanías deun valor óptimo.Así como existe una única recta que pasa por dos puntos, hay únicamente una ecuacióncuadrática que pasa por tres puntos. De esta forma, si se tienen tres puntos que contienen unpunto óptimo, se ajusta una parábola a los puntos, después se puede derivar e igualar a cero,y así obtener una estimación del óptimo.x* ()()()2222221 f (x 0 ) x1 x 2 f ( x1 ) x 2 x 0 f ( x 2 ) x 0 x1 2 f ( x 0 )(x1 x 2 ) f (x1 )(x 2 x 0 ) f (x 2 )( x 0 x1 ) Este método utiliza evaluaciones de la función, y sólo un nuevo valor de función debe sercalculado en cada iteración.Interpolación cúbicaEste método está basado en la aproximación polinomial mediante un polinomio de tercergrado de la función que se quiere minimizar. El esquema es similar al método cuadrático.Se necesitan cuatro puntos iniciales, o cuatro valores de f(x), o valores de f(x) y susderivadas cada dos puntos.9
Procesos Químicos IIEste método es de convergencia rápida, pero puede presentar errores en funciones nounimodales.Dados xk-1 y xk junto a f(xk-1), f’(xk-1), f(xk), y f’(xk) es posible ajustar una ecuación cúbica enlos puntos. El punto xk 1 (mínimo) puede ser determinado como el punto mínimo relativo deesta ecuación cúbica. f ′(x k ) µ 2 µ1x k 1 x k (x k x k 1 ) f ′( x k ) f ′(x k 1 ) 2 µ 2 f ( x k 1 ) f ( x k )µ1 f ′(x k 1 ) f ′( x k ) 3x k 1 x k[]µ 2 µ1 2 f ′(x k 1 ) f ′( x k )12La aplicación de éste método requiere que xk-1 xk y f (xk) f (xk-1).10
Procesos Químicos IIMétodos indirectosEjemplo:Minimizar la siguiente función utilizando los métodos indirectos vistos anteriormente:f (x ) 2 x 2 16x1. Resolución utilizando el método de NewtonEl punto de partida es x0 1, el método converge en 3 iteracionesIteración01234Método de Newtonxkf (xk)f 1915,1192. Resolución utilizando el método de Quasi-NewtonEl paso utilizado fue h 0.01, el método converge en 3 iteraciones.Iteración01234Método de Quasi-Newtonxkf(x xk)1815,555515,131215,119115,11913. Resolución utilizando el método de la 7261,6441,6101,5971,591Método de la Secantef (xq)x*2,53119,361,936 7,624011,72579 3,474851,64367 1,53111,61048 0,652351,59690,2731,59132 0,113321,58902 0,04687f 815,13815,12215,12015,11915,119El intervalo utilizado para optimizar la función fue (1,5), el valor óptimo se obtiene luego de6 iteraciones.11
Procesos Químicos IIMétodos directos, eliminación de regionesEjemplo:Diseño de un intercambiador de calor, minimizando los costos anuales (“Productand process design principles. Synthesis, analysis, and evaluation”, Seider W., Seader J., Lewin D., 2004 2ªEdition, pp 628-629. Ed. John Wiley and Sons Inc.)En una refinería de petróleo, 80000 lb/hr de un gas ligero que salen de una torre dedestilación de crudo a 440ºF, son actualmente enfriados utilizando agua, antes de seralmacenados. El calor perdido podría ser utilizado para precalentar 500000 lb/hr de petróleocrudo, el cual se dispone a 240ºF y se calienta utilizando otros medios a un costo de 3/million Btu, la planta opera 8200 hr/año. Basándose en los siguientes datos determine quedebe hacerse. Cp del gas ligero: 0.5 Btu/lb ºFCp del petroleo crudo: 0.45 Btu/lb ºFCosto anual de operación: Cop 0.8248 Cp{A}Cp{A}: exp[11.667-0.8709 Ln(A) 0.09005intercambiador, ft2U: 24.5 Btu/hr ºF ft2[Ln(A)]2],A: área delPlanteo de la función objetivo:Los costos de operación están relacionados con el calor intercambiado, comenzamos porplantear los balances de energía:Q 80000(0.5)(440 TLGO ,out )Q 500000(0.45)(TCO ,out 240 )Balance de energía en el intercambiador:Q 24.5 A(440 TCO , out) (TLGO , out 240 ) 440 TCO ,out Ln 240T LGO,out Nuestro objetivo es minimizar el costo anual de operación, la función objetivo será:C A 0.0246 * Q 0.8248 * C p {A}En los planteos realizados hay variables que no se conocen, una de ellas será nuestra variablede decisión. La mejor elección es la temperatura de salida del gas ligero, debido a que estapuede tomar valores limitados y permite calcular secuencialmente el resto de las variables. Elvalor superior de la temperatura de salida del gas es de 440ºF, en este caso el costo seríanulo, el límite inferior es 240ºF, temperatura de entrada del petróleo crudo, el costo seríainfinito.1. Resolución por el método de Fibonacci, la tolerancia utilizada fue de 5%.12
Procesos Químicos IIPunto TLGO, 058268,57Fibonacci, tolerancia 5%62A [ft ]TCO, out Q x 10 560,61684,83535,62560,64320,83535,63CA x 10 [ 6,8La solución óptima del sistema se alcanza en la iteración número 7. La temperatura de salidadel gas ligero óptima encontrada es de 259.05 ºF, el valor del costo anual es de -141.9 103 /año, es decir que la instalación de intercambio de calor provocaría un ahorro. Si sedisminuye la tolerancia especificada puede lograrse un valor de temperatura más cercano alóptimo, pero en ese caso el número de iteraciones aumenta.2. Resolución por el método de la Sección AureaPunto1234567Sección Aurea6TLGO, out TCO, out Q x 10 [BTU/Hr]A [ft ]CA x 10 [ 23La solución óptima del sistema se alcanza en la iteración número 6. La temperatura de salidadel gas ligero óptima encontrada es de 251.1 ºF, el valor del costo anual es de -144.2 103 /año. La velocidad de convergencia de este método es superior al método de Fibonacci.3. Resolución por el método de la Dicotomía, en este caso el valor de x utilizado fue de10ºFPunto123456789Método de la dicotomía, x 10623TLGO, out TCO, out Q x 10 [BTU/Hr] A [ft ] CA x 10 [ -138,6En este caso el valor de temperatura de salida del gas ligero, que optimiza nuestra funciónobjetivo, se obtiene luego de 8 iteraciones.13
Procesos Químicos II4. Resolución por el método de búsqueda secuencial con dos experimentos igualmenteespaciadosEl valor óptimo se obtiene con 15 iteraciones. Puede observarse que de los tres métodosutilizados para la resolución del problema planteado, el método de la sección Áurea poseeuna velocidad de convergencia superior.Busqueda secuencial con dos exp. igualmente espaciados623A [ft ]CA x 10 [ /año]Punto TLGO, out TCO, out Q x 10 [BTU/Hr]1306,67 263,705,331931,0-108,32373,33 251,852,67683,8-50,43284,44 267,656,222691,1-125,84328,89 259,754,441403,7-89,65269,63 270,296,813465,6-136,16299,26 265,025,632150,0-114,37259,75 272,047,214250,1-141,68279,51 268,536,422914,8-129,49253,17 273,217,475041,3-143,910266,34 270,876,953692,6-138,111248,78 273,997,655837,1-144,112257,56 272,437,304479,3-142,613245,85 274,527,776636,0-142,814251,71 273,477,535272,1-144,115249,75 273,827,615630,0-144,216253,66 273,137,454970,1-143,85. Resolución por el método de búsqueda preplaneada, localizando el valor optimo dentrodel 5% del rango inicial.En este caso los experimentos deben realizarse todos al mismo tiempo, el número deexperimentos a realizar esta determinado por la tolerancia, que en este caso es del 5%.N 2 10.05N 39i(440 240)º F, donde i indica el número de experimento, y N el número totalN 1de experimentos.Ti 240º F Una vez realizados todos los experimentos se determina el intervalo que contiene el valoróptimo. En este caso el óptimo de temperatura se encuentra entre (245ºF,255ºF).14
Procesos Químicos IIPunto TLGO, 435,00Búsqueda Preplaneada, tolerancia 5%623A [ft ]CA x 10 [ /año]TCO, out Q x 10 -12,5-7,9-3,02,08,2
Procesos Químicos IIMétodos de aproximación polinomialEjemplo:Minimizar la siguiente función utilizando los métodos de aproximación polinomialanalizados:f (x ) 2 x 2 16x1. Resolución utilizando el método interpolación cuadráticaLos puntos iniciales utilizados fueron x0 1, x1 2.5 y x2 5, el método converge en cuatroiteraciones, el valor óptimo obtenido es x* 1.60.x0Iteración01341111Interpolación cuadráticax2f(x1)f(x0)x*2,551,661818,91,66 2,5 1,701815,1491,66 1,7 1,611815,1491,61 1,7 015,12215,1202. Resolución utilizando el método interpolación cúbica.Para éste método se necesitan dos puntos iniciales, y los respectivos valores de la derivada dela función, dichos valores iniciales fueron x0 1, x1 2. El método converge en la terceraiteración, el valor óptimo es x* 1.59.Interpolación cúbicau1u2f 49
Procesos Químicos IIBibliografía Beveridge G., Schechter (1970) “Optimization: Theory and Practice” Ed. McGraw-Hill. Castillo E., Conejo A., Pedregal P., García R., Alguacil N. (2002), “Formulación yResolución de Modelos de Programación Matemática en Ingeniería y Ciencia” . Chapra Steven, Canale Raymond (2006). “Numerical methods for engineers”, 5th edition.Ed. McGraw-Hill. Edgar T., Himmelblau. (1988) “Optimization of chemical processes” Ed. McGraw-Hill. Reklaitis G., Ravindran A., Ragsdell K. (1983), “Engineering Optimization. Methods andApplications”, Ed. John Wiley and Sons Inc. Tarifa E. (2006) “Optimización y Simulación de Procesos. Métodos numéricos” Facultadde Ingeniería - Universidad Nacional de Jujuy Zerpa L., Colmenares J. (2004), “Optimización para ingenieros, optimización sinrestricciones”. Notas de clase, Universidad del Zulia, Facultad de Ingeniería, División deEstudios para Graduados, Instituto de Cálculo Aplicado. República Bolivariana deVenezuela. Seider W., Seader J., Lewin D., (2004), “Product and process design principles.Synthesis, analysis, and evaluation”, 2ª Edition, Ed. John Wiley and Sons Inc.17
Métodos numéricos para optimización de funciones de una variable Para la aplicación de estos métodos es necesario conocer el intervalo inicial 0 donde esta contenido el óptimo de la función objetivo, y asegurar la unimodalidad de la función en el intervalo en estudio. Un método de optimización para una función de una sola variable .