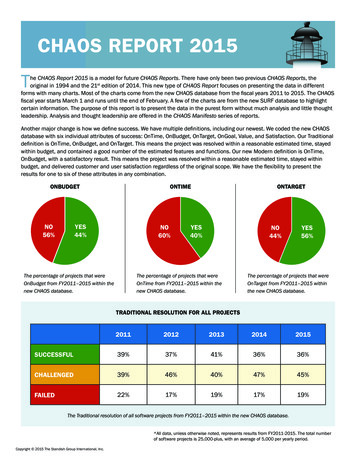
Transcription
Understanding the Role of Chaos Theory inMilitary Decision MakingA MonographbyMAJ Donovan O. FuquaUnited States ArmySchool of Advanced Military StudiesUnited States Army Command and General Staff CollegeFort Leavenworth, KansasAY 2009Approved for Public Release; Distribution is Unlimited
Form ApprovedOMB No. 0704-0188REPORT DOCUMENTATION PAGEPublic reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources, gathering and maintaining the dataneeded, and completing and reviewing this collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information, including suggestions for reducing this burden toDepartment of Defense, Washington Headquarters Services, Directorate for Information Operations and Reports (0704-0188), 1215 Jefferson Davis Highway, Suite 1204, Arlington, VA 22202-4302. Respondentsshould be aware that notwithstanding any other provision of law, no person shall be subject to any penalty for failing to comply with a collection of information if it does not display a currently valid OMB control number.PLEASE DO NOT RETURN YOUR FORM TO THE ABOVE ADDRESS.1. REPORT DATE (DD-MM-YYYY)2. REPORT TYPE3. DATES COVERED (From - To)21-05-2009MonographJuly 2008 – May 20094. TITLE AND SUBTITLE5a. CONTRACT NUMBERUnderstanding the Role of Chaos Theory in Military Decision Making5b. GRANT NUMBER5c. PROGRAM ELEMENT NUMBER6. AUTHOR(S)5d. PROJECT NUMBERMAJ Donovan O. Fuqua5e. TASK NUMBER5f. WORK UNIT NUMBER7. PERFORMING ORGANIZATION NAME(S) AND ADDRESS(ES)8. PERFORMING ORGANIZATION REPORTNUMBERAdvanced Military Studies Program250 Gibbon AvenueFort Leavenworth, KS 66027-21349. SPONSORING / MONITORING AGENCY NAME(S) AND ADDRESS(ES)10. SPONSOR/MONITOR’S ACRONYM(S)Command and General Staff College1 Reynolds AvenueFort Leavenworth, KS 66027CGSC, SAMS11. SPONSOR/MONITOR’S REPORTNUMBER(S)12. DISTRIBUTION / AVAILABILITY STATEMENTApproved for Public Release; Distribution is Unlimited13. SUPPLEMENTARY NOTES14. ABSTRACTChaos theory is a poorly understood concept in social science and in military analytical decision making systems. Militarydecision makers require a multidisciplinary approach of mathematical analysis, modeling and simulation, topology, and poststructural philosophy if they intend to conceptualize chaos theory and complex adaptive systems and theirs relevance to militaryplanning. The essence of this understanding is that while chaos appears random, chaos properly understood is a deterministicseries found in very simple forms. These forms exhibit sensitivity to initial conditions, bounding, and attractors.Understanding chaos has several applications for military planning in real world environments. Because chaos is bounded,planners can create allowances for system noise. The existence of strange and normal chaotic attractors helps explain why systemturbulence is uneven or concentrated around specific solution regions.15. SUBJECT TERMSChaos Theory, Decision Making, Complexity Theory, Complex Adaptive Systems16. SECURITY CLASSIFICATION OF:a. REPORTb. ABSTRACTc. THIS PAGE(U)(U)(U)17. LIMITATIONOF ABSTRACT18. NUMBEROF PAGESStefan J. Banach, COL, US Army19a. NAME OF RESPONSIBLE PERSON(UU)5419b. TELEPHONE NUMBER (include areacode)913-758-3302Standard Form 298 (Rev. 8-98)Prescribed by ANSI Std. Z39.18
SCHOOL OF ADVANCED MILITARY STUDIESMONOGRAPH APPROVALMajor Donovan O. FuquaTitle of Monograph: Understanding the Role of Chaos, Adaptation, and Dynamic Turbulence inMilitary Decision MakingApproved by:William J. Gregor, Ph.D.Monograph DirectorAlex Ryan, Ph.D.Monograph ReaderStefan J. Banach, COL, INDirector,School of AdvancedMilitary StudiesRobert F. Baumann, Ph.D.Director,Graduate DegreeProgramsii
AbstractUNDERSTANDING THE ROLE OF CHAOS THEORY IN MILITARY DECISION MAKING by MAJORDonovan O. Fuqua, US Army, 54 pages.Chaos theory is a poorly understood concept in social science and in military analytical decision makingsystems. Military decision makers require a multidisciplinary approach of mathematical analysis, modeling andsimulation, topology, and post-structural philosophy if they intend to conceptualize chaos theory and complexadaptive systems and theirs relevance to military planning. The essence of this understanding is that while chaosappears random, chaos properly understood is a deterministic series found in very simple forms. These forms exhibitsensitivity to initial conditions, bounding, and attractors. Despite various methods for detecting chaos in mechanicalsystems, data set size limitations and inability to separate out adaptive behaviors make these techniques of littlevalue in situ.Adaptation and complexity are phenomena that are very different from chaos. Higher order interactions andeffects, self-organization, and propensity of co-evolution and novel emergence distinguish chaos from stochasticprocesses. The self-organization and emergence are evident when a cumulative effect is different from the additiveeffects of the components. These self-organizing components differ from chaos because the properties of resolutionand scope are fundamentally different. The fractal nature of chaos ensures that it is scale less and, therefore, unableto produce novel emergent effects.One way to conceptualize chaos within complexity is through the Deleuzian post-structural Philosophy ofDifference regarding Smooth and Striated Spaces and Nomad versus the Sedentary agents. This conceptualization,transferred to chaos applications, links turbulence to barriers and increased gridding on the surface of open systems.These barriers inform agents on suitable terrain and options during decision-making.Understanding chaos has several applications for military planning in real world environments. Because chaosis bounded, planners can create allowances for system noise. The existence of strange and normal chaotic attractorshelps explain why system turbulence is uneven or concentrated around specific solution regions. Finally, thepresence of chaos limits the effectiveness of single variable variation reduction techniques such as Lean Six Sigmabecause of unpredictable system behavior.iii
TABLE OF CONTENTSIntroduction . 1Chaos Theory Overview . 6One Variable Chaos . 7Multiple Variable Chaos . 13Detection and Applications of Chaos and Fractals . 17Fourier Analysis . 18Lyapunov Trajectory Analysis . 19Kolmogorov-Sinai Entropy Analysis . 20Examples of Chaos Detection in Military Operations . 22Fractals . 23Military Operations: Adaptive, Complex, and Dynamic . 25How Chaos Differs From and Influences Adaptive Systems. 32Conceptual Model of Chaos in Complex Adaptive Systems . 33Conclusion and Topics for Further Research . 38Appendix 1: Definitions . 41Appendix 2: Program Coding for Monograph . 44Bibliography . 52iv
Table of FiguresFigure 1: Graphical Representation of "The Race Track" . 2Figure 2: Null and Alternative Hypotheses. 4Figure 3: One Variable Chaos - Sensitivity to Initial Conditions, x(0) 1.0 . 8Figure 4: One Variable Chaos – Sensitivity to Initial Conditions, x(0) 0.5. 8Figure 5: The Logistics Equation: The Move to Chaos through Period Doubling, K 0.5 . 10Figure 6: The Logistics Equation: The Move to Chaos through Period Doubling, K 2.0 . 10Figure 7: The Logistics Equation: The Move to Chaos through Period Doubling, K 3.0 . 11Figure 8: The Logistics Equation: The Move to Chaos through Period Doubling, K 3.6 . 11Figure 9: Quasiperiodicity Caused by Three Sine Functions with Different Frequencies . 12Figure 10: NetLogo Simulation of Lotka-Volterra Equations . 14Figure 11: MatLab Simulation of Lorenz Equations: The Butterfly Effect . 16Figure 12: Simple Supply Chain Network . 25Figure 13: Linear Program for Simple Supply Chain Network Model . 26Figure 14: Segregation Model at Time 0 . 30Figure 15: Effect of Changing a Parameter in the Segregation Simulation . 31Figure 16: Conceptual Model for Understanding Chaos as a Part of Adaptive Systems . 34v
IntroductionAnnually, the US Army Combined Arms Center prepares a list of research topics. The list isdistributed to the students enrolled in the Command and General Staff College to encourage research inareas of interest to the Army. Among the topics found in the AY2008-09 research list was a questionasking whether Chaos Theory was applicable for understanding Army sustainment operations. The topicmay have only reflected a general curiosity that many have for Chaos Theory because many researchershave tried to apply chaos theory to understand a variety of business and academic activities. It might alsoreflect the interest in the Army logistics community in contemporary business methods and by extension,chaos theory. Regardless of the motive for listing the topic, it strongly suggests that military leaders needto learn more about Chaos Theory before leaping into logistic applications.Military decision makers tend to view the real world in terms of direct causal relationships andlinear effects. One example is from personal experience as a transportation brigade operations officer(S3) working to support deployment and distribution during Operation Iraqi Freedom. During theoperations, a higher headquarters attempted to build a chart called “the race track” to track theperformance of the container distribution system from depots in the United States and Germany throughKuwait and into Iraq and back to the United States and Germany. The higher command wanted eachdecision maker to focus on decreasing delivery time. However, the casual and linear paradigm wasinsufficient for explaining and predicting the environment.Despite the effort to control every transportation process, delivery times exhibited aperiodicvariation. Through analysis of the port clearance times, transit times, and hold times at each stop, theplanners could not attribute the variation to changes in procedures at any location. Although the higherheadquarters was pleased with an overall reduction of the mean time for transit, variation in materieldelivery time continued to be a problem since forward deployed units tended to stockpile equipment or1
extend deployment or redeployment timelines based upon imprecise guaranteed delivery times. Theseaperiodic variations were seemingly beyond the operators’ control, but were definitely part of agingThe Distribution“Race Track”USStagingIraqFOBStartFinishUSDepotor FortIraqDeliveyFigure 1: Graphical Representation of "The Race Track"One way to view “the race track” problem is through systems theory and analysis. In systemsthinking, locations, actors, and routes are conceptualized as nodes, adaptive agents, and arcs. By framingthe problem as a mental model, the command could have conducted analysis on the source of thevariation. However, systems framing requires choices on what to include and what to ignore to develop apredictive model of reality. A frame that includes only adaptive elements will not generate an adequaterepresentation of reality due to the exclusion of physical phenomena with chaotic or fractal components.Decision makers must consider including fractal and chaotic components as in any model intending tomirror reality.Unfortunately, the concept of chaos is poorly understood within most business, social science,and military literature and casual vernacular. The confusion is generated by the failure to distinguish2
between stochastic randomness and mathematical determinism. 1 The phenomenon of chaos and chaostheory refers to the the technical mathematics definition of a dynamic deterministic process that appearsrandom. 2 Based on its deterministic nature however, the short term past and future behavior of chaoticsystems can be known exactly through calculation, even though the output appears random. 3Unfortunately, the deterministic nature of chaos theory recalls the commander of US Joint ForcesCommand recent criticisms of Effects Based Operations (EBO). 4 If chaos were examined as the solemechanism in complex systems, the argument would be that through perfect knowledge of the model,decision makers would precisely know the future states and behaviors of the system. By reducing thesystem to its components, planners would have perfect predictive abilities. This reductivist argument doesnot actually describe the characteristics of open systems. Open systems are comprised of multipleadaptive elements with complex interactions that result in highly ordered effects and the potential fornovel emergent properties. Unfortunately, limiting a system frame to adaptive elements does notaccurately describe chaos in nature, where small fluctuations in initial conditions and changes inparameters have radical changes to system behaviors.Decision makers should consider chaos as a possible superficial element of complex adaptivesystems that can create system noise and first order effects 5 but not direct self-organization or novel1When a variable has an associated probability density, it is stochastic. Stochastic is derived from a Greekword meaning ‘guess’ and refers to randomness. While the exact value of a stochastic variable is random, it can takevalues within a set distribution with a mean and variance (a probability density).2It is important to note that the models presented imply perfect system knowledge and infinite resolution.In infinite resolution, chaos is not random. However, when the start point is unknown and resolution is finite, chaoscan be a source of actual randomness. This is an important point that separates the models from real worldphenomena. The models explain the mechanics of chaos, not to predict real events.3A system is an abstraction of reality – a mental model used to explain and simplify the real world.Systems are an arrangement or a set of autonomous and interrelated entities, parts, units, components and variablesthat form an integrated whole.4GEN James Mattis, “Assessment of Effects Based Operations”, Memorandum, (United States JointForces Command, Norfolk, Virginia, 14 August 2008).5 Ordered effects can refer to the degree of interaction between elements to generate an effect. First ordereffects are caused by additive properties of the elements, where there is no interaction effect. Higher ordered effectsoccur when elements interact to form a nonadditive effect. For example:is first order when x3
emergence. Because all chaos is derived from mechanical or deterministic mechanisms, when consideredin isolation, chaos theory has little relevance for military decision making. From the systems perspective,decision makers should consider chaos as a component of complex adaptive systems. Using thisframework, chaos and other forms of deterministic turbulence can form the first order structure of smoothand striated spaces in open systems. 6 This, in effect, has the potential to create system noise and lowresistance regions (smooth space) and high resistance regions (striated space). These regions help formthe macrostructure of the system, and can guide first order adaptive behavior.Based on a systems framework, chaos and other forms of deterministic turbulence affect complexadaptive systems through inputs and outputs that influence first order system structure. The nullhypothesis is that deterministic turbulence has no effect on open complex systems because adaptiveentities entirely mask non-adaptive portions. These hypotheses are labeled:::the behavior ofFigure 2: Null and Alternative HypothesesThe hypotheses are tested using both qualitative and quantitative analysis. This methodologyutilizes computer simulation, philosophical reasoning, and real-world case study examination. Thesemethods compare and contrast the behaviors of adaptive systems to chaos systems both in situ and insilica 7 . While the argument contains mathematical and system analysis, the intended audience is militaryand y are variables and a and b are constants.is a second order effect due to the singleinteraction between x and y.6Smooth and striated spaces refer to Gilles Deleuze and Felix Guttari’s concepts of the nature of spaces inA Thousand Plateaus. In the book, they use smooth and striated in many different contexts. The one used in themonograph refers to freedom of movement. Smooth space is analogous to the ocean or a desert; where movement isunhindered due to lack of obstacles. Striated Space is analogous to a heavily populated city or a sharp mountainrange. Heavily striated space limits maneuver or choices.7In situ is a Latin phrase that means ‘in the place’. It refers to an observation or experiment in a natural orordinary setting. In contrast, in silica refers to a experiment or observation that occurs in a computer setting, such asa computer simulation. Both offer advantages and disadvantages. While systems viewed in situ show actualbehavior, it is difficult to change conditions and experiment. In silica experiments allow changes and multipleiterations, but can often ignore key elements that influence system behavior.4
planners who want to better understand the concept of chaos and how it fits into the decision makingprocess.Through an examination of the history, structure, and outcomes of chaos, the reader gains acommon frame of reference for understanding chaos theory. In order to understand chaos theory, militarydecision makers must have a common definition and an understanding of the history and physicalapplications of chaos. Increasingly complex models show provide background to the reader. Rudimentarymodels such as the one variable logistics equation give a basic understanding while more complicatedmodels with two and three variable differential equations better mimic real world phenomena. Thesemodels give better understanding of the implications of chaos: sensitivity to initial conditions, strangeattractors, and constants of motion. By showing the routes that lead relatively simple models to chaos,planners can recognize that small shifts can cause radically different behaviors.Once the planner has an understanding of the basic mechanics of chaos, it is possible to considerapplications and detection methods. Using those methods permits investigation of a variety of cases. Thecases considered include the use of autocorrelation, Fourier analysis, and Kolmorgov-Sinai entropyequations. The point of the analysis is to show the difficulties and data set limitations in predicting andcontrolling chaos. The discussion next teurns to fractal geometry and power laws because they are relatedto chaos. While these systems are deterministic, they have different behaviors, detection methodologies,and slightly different implications for planning.As stated, chaos in isolation is worthless to a miltiary planner because it only describesdeterministic and mechanistic effects. Therefore, real-world military operations are almost alwaysconducted in open complex environments. Based upon that frame, there are definite possiblecharacteristics of complex adaptive interactions: novel emergence, co-evolution, and self-organization.After describing these traits, it was important to use computer simulation to show in silica how novelbehavior is generated. Based upon analysis through basic topology, systems thinking, and philosophy, themonograph shows how chaos can influence first order system behavior but cannot cause emergence andother traits associated with higher ordered behavior.5
Based on this understanding, planners must conceptualize the influence of chaos on complexadaptive systems. A proposed model outlines the implications of chaos properties such as sensitivity toinitial conditions and attractors. This understanding then generates possible tools for decision making andcontrol of complex systems with adaptive and chaos components.Chaos Theory OverviewChaos theory is a relatively new branch of mathematics that is expressed in completelydeterministic motion equations. 8 Although chaos is a mathematical model, it is important to note that realworld environments have behaviors that can be explained and predicted through the use of chaos theory.The fact that military operations occur in situ obligates planners to consider the periodic effects ofphysical phenomena. Weather patterns, waves, and other physical motion can have varied effect onoperations. For example, it is impossible to analyze sea port of debarkation (SPOD) activities withoutconsidering tides, wave patterns, and storms. Therefore, decision makers must understand the history,definitions, and some basic examples of chaos to illustrate the concepts of sensitivity to initial conditions,system attractors, and bounded strange attractors.When a decision maker looks at a random-appearing data set, the two questions that shouldimmediately arise are: what caused this behavior and what does it mean to the operation. Chaos theory isone tool used to understand the phenomenon of system turbulence. While the theory is definitely not aperfect tool, systemic analysis offers distinct improvements over simply disregarding the behavior andmaking suboptimal decisions based on a lack of understanding.Chaos is random-like behavior with certain necessary but not sufficient criteria. In order to beconsidered chaos, a system must be bounded, nonlinear, sensitive to small changes in the initial8Edward Lorenz and other scientists developed deterministic models to explain random-like behavior overa time series starting in 1963. Although the genesis of Chaos Theory is over 40 years old, in mathematics, thatconstitutes a relatively new field. James Gleick, Chaos, Making a New Science. (Viking Penguin, New York, 1987),5.6
conditions, and dynamical. 9 Those ingredients do not guarantee chaos, but give the basic components thatallow a deterministic system to be driven into random-like behavior. The important point of chaos is thatit is random-like.True random behavior is a stochastic mechanism that resembles Brownian movement, also calleda random walk. 10 If you rolled a fair six-sided die, you would have an equal chance of hitting any side,however, there would be no way of predicting what the next throws would generate. A way to visualizethis is to ask a classic statistics question: if you rolled a ‘six’ fifty times in a row, what would be thechance of rolling a ‘six’ on the fifty first roll? The answer is that you would have a one-sixth chancebecause each roll is an independent random event. The next event in chaos, however, is completelydetermined by the last event and that system is greatly influenced by initial conditions. In order tounderstand this phenomenon and show that chaos is not a dense, impeneratrable branch of theoreticalmathematics, three simple one-variable systems simulate chaos.One Variable ChaosChaos can be modeled using a relatively simple one-variable nonlinear difference equation. 11 Inreal environments these behaviors are manifest as simple birth-death rates, limited carrying capacities, orthe spread of a disease. Equation 1 is a one variable difference equation where the next value of thevariable ‘x’ is generated by an operation to the previous variable value. This system is easily simulatedand graphed in Microsoft Excel by selecting different start points (0.5 and 1.0) to show sensitivity toinitial conditions. 129Glenn E. James, Chaos Theory: The Essentials for Military Applications, (Naval War College, Newport,1997), 38.10Brownian movement refers to truly random behavior. It is named for Robert Brown, a Scottish Biologist,who described the movement of a particle in a liquid as a random walk, where the direction and length of a stepcannot be determined by any of the previous steps.11A difference equation models future discrete states given an operation applied to the current discretestate.12Model adapted and simulated based on simple equations suggested in C Gregobi, Crises, “SuddenChanges in Chaotic Attractors, and Transient Chaos”, Physica D7, (1984), 632-638.7
xt 1 1.9 xt2X ValueEquation 1, X(0) 1.02.521.510.50‐0.5‐1‐1.5‐21 2 3 4 5 6 7 8 9 101112131415161718192021Iteration TFigure 3: One Variable Chaos - Sensitivity to Initial Conditions, x(0) 1.0Equation 1, X(0) 0.52.521.5X Value10.50‐0.51 2 3 4 5 6 7 8 9 101112131415161718192021‐1‐1.5‐2Iteration TFigure 4: One Variable Chaos – Sensitivity to Initial Conditions, x(0) 0.5While the equation is the same in both graphs (Figures 3 and 4), system behavior is radicallydifferent given a change in initial conditions. This symptom of chaos also explains the idea that whileshort-term behavior can be predicted, long-term prediction of specific points becomes impossible. Inchaotic physical systems, any perturbation can change long-term behavior.8(1)
Long-term system motion and dynamics can be relatively predictable in controlled environments.In the graphs, while the individual points are scattered, the system behavior is bounded in that no valueexceeds the absolute value of the parameter 1.9. Therefore, despite the turbulence of the individual points,the general system behavior is predictable – it varies between -1.9 to 1.9 as long as x is less than or equalto 1.The second powerful implication of chaos is the concept of the attractor. Three types of attractorsdeserve mention: the point attractor, the periodic attractor, and the strange attractor 13 . While there are keydifferences in each, they imply that chaos systems can exhibit steady states over time. By understandingthis concept, it is possible to understand why a turbulent system can exhibit two or more phases.The best way to begin to explain the concept of attractors is through an examination of thelogistics equation. 14 This is a nonlinear difference equation in the general form (Equation 2) where k isthe parameter and x is the variable. 15 For low parameter values where k 1, the points converge to asingle point zero. This is a point attractor of the system. When 1 k 3, solutions are driven to nonzeropoint attractors. 16 At k 3, the equation exhibits a bifurcation and exhibits two alternating points. When k 3, the system rapidly moves into chaos, where period doubling occurs according to an approachedconstant. This constant, the Feigenbaum number, approaches a limit (Equation 3 where period doublingoccurs at a parameter valueand the next period doubling occurs at. This limit approximates thenext critical parameter value where period doubling can be anticipated. Figures 5 through 8 illustrate thephenomenon of period doubling as a route to chaos.1(2)13An attractor is defined as a phase space point or set of points representing the various possible steadystate conditions of a system. An equilibrium state or group of states to which a dynamical system converges. GarnettWilliams Chaos Theory Tamed, (Joseph Henry Press, Washington, 1997), 447.14In this usage, logistic refers to the shape of the growth curve rather than the military usage implying thecontrol of supply and distribution. Although the continous formulation of the logistics equation is not chaotic, theequation is highly useful as an example to illustrate period doubling.915Garnett Williams Chaos,, 162.16Ibid., 164-165.
lim 4.6692Equation 2, X(0) .4, K 0.50.5X Value0.40.30.20.101 2 3 4 5 6 7 8 9 101112131415161718192021Iteration TFigure 5: The Logistics Equation: The Move to Chaos through Period Doubling, K 0.5X ValueEquation 2, X(0) .4, K 2.00.70.60.50.40.30.20.101 2 3 4 5 6 7 8 9 1011121314151617181
School of Advanced Military Studies . United States Army Command and General Staff College . Fort Leavenworth, Kansas . Chaos theory is a poorly understood concept in social science and in military analytical decision making systems. Military decision makers require a multidisciplinary approach of mathematical analysis, modeling and .