WIXLIB

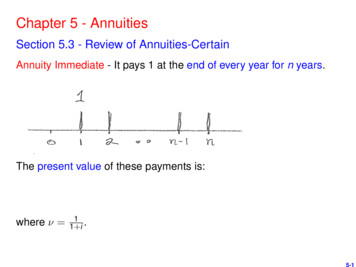
Chapter 5 - AnnuitiesSection 5.3 - Review of Annuities-CertainAnnuity Immediate - It pays 1 at the end of every year for n years.The present value of these payments is:where ν 11 i .5-1

Annuity-Due - It pays 1 at the beginnig of every year for n years.The present value of these payments is:where d i1 i .5-2

Continuous Payment Annuity - It smears the payment of 1 over eachyear for n years.The present value of this smear of payments is:where δ ln(1 i).5-3

mth ly Annuity Immediate - It paysyear for n years.1mat the end of every1mpart of theThe present value of these payments is:where 1 i(m) mm (1 i) ν 1 .5-4

mth ly Annuity Due - It paysyear for n years.1mat the beginning of every1mpart of theThe present value of these payments is:where 1 d(m) mm (1 i) ν 1 .5-5

Section 5.4 - Annual Life AnnuitiesThe annual life annuity pays the annuitant (annuity policyholder)once each year as long as the annuitant is alive on the paymentdate. If the policy continues to pay throughout the remainder of theannuitant’s life, it is called a whole life annuity.Subsection 5.4.1 - Whole Life Annuity-DuePayments of 1 are made at the beginning of each year of theannuitant’s remaining life. The present value random variable is5-6

The only random part of this expression is ν Kx 1 . We have alreadyfound in chapter 4 (pages 4-6, 4-7) that E ν Kx 1 Axand 2 2E ν Kx 1 Ax .Because Y is a linear function of ν Kx 1 , we immediately get the EPVand Var[Y] to be5-7

An alternative expression for the EPV can be found by noting thatY I(Tx 0) νI(Tx 1) ν 2 I(Tx 2) · · ·,where I({event}) 1 if the event occurs and 0 otherwise.Clearly,We also note thatY (1)I(0 Tx 1) (1 ν)I(1 Tx 2) (1 ν ν 2 )I(2 Tx 3) · · ·or5-8

Y Xäk 1 I(k Tx k 1).k 0This producesA whole life annuity-due could be used to describe annual paymentsfrom an insurance company to an individual under a lifetime annuitycontract. It can also be used to describe the annual premiums paidby an individual to the insurance company which is used to fund theindividual’s life insurance.5-9

Subsection 5.4.2 - Term Annuity-DueThe present value random variable of 1 annual payments under anannuity due contract with a maximum of n payments is: äKx 1 if Kx nY än if Kx n 1 ν min(Kx 1,n).dIt follows that the EPV isNote that Ax:n is the endowment insurance EPV. See page 4-21.5-10

This EPV can also be written asäx:n n 1Xν k k pxork 0The variance of Y can be written as" n 1#X Var [Y ] (äk 1 )2 k qx (än )2n px 2 äx:n .k 0A term annuity-due is often used to describe the annual premiumspaid by an individual to the insurance company which is used to fundthe individual’s life insurance in settings which have a maximumnumber of premium payments.5-11

Subsection 5.4.3 - Whole Life Annuity-ImmediateIn this setting 1 annual payments are made at the end of each yearprovided the annuitant is alive at that point in time.Denote the present value random variable of these payments byY νI(Tx 1) ν 2 I(Tx 2) · · ·,Comparing this expression to Y described at the top of page 5-6,shows thatY Y 1.Therefore, the expected value and the variance satisfy5-12

Subsection 5.4.4 - Term Annuity-ImmediateIn this setting the 1 annual payments are made at the end of eachyear provided the annuitant is alive at that point in time, but there willbe at most n payments made. The present value random variable isYn νI(Tx 1) ν 2 I(Tx 2) · · · ν n I(Tx n), amin(Kx ,n) 1 ν min(Kx ,n).iIt follows that its EPV isComparing this toäx:n n 1Xνkk px ,k 05-13

we see thatSinceYn " n 1X#ak I(k Tx k 1) an I(Tx n),k 1the variance of Yn can be written asVar [Yn ] " n 1X#2(ak )kqx (an )2n px 2 ax:n .k 15-14

Example 5-1: You are given 10 p0 .07, 20 p0 .06 and 30 p0 .04.Suppose each survivor age 20 contributes P to a fund so there is anamount at the end of 10 years to pay 1,000 to each survivor age30. Use i .06 and find P.Example 5-2: You are given (1) 10 year pure endowment of 1, (2)whole life annuity-immediate with 1 annual payments, (3) whole lifeannuity-due with 1 annual payments and (4) 10-year temporary lifeannuity-immediate with 1 for annual payments. Rank the actuarialpresent values of these options.5-15

Example 5-3: An insurance company agrees to make payments tosomeone age x who was injured at work. The payments are 150Kannually, starting immediately and continuing as long as the personis alive. After the first 500K the remainder is paid by a reinsurancecompany. Let i .05, t px (.7)t for 0 t 5.5 and 0 for t 5.5.Calculate the EPV for the reinsurance company.5-16

Example 5-4: You are given: P[T0 25] .7 and P[T0 35] .5 .Each of the following annuities-due have an actuarial PV of 60,000:(1) life annuity-due of 7,500 on (25)(2) life annuity-due of 12,300 on (35)(3) life annuity-due of 9,400 on (25) that makes at most 10 paymentsWhat is the interest rate?5-17

Section 5.5 - Annuities Payable ContinuouslySubsection 5.5.1 - Whole Life Continuous AnnuityIn this setting a continuous payment of 1 is smeared over each yearuntil time t (not necessarily an integer). The present value of thissmear isZ tνt 11 νtνs t at ν s ds ln(ν) 0ln(ν)δ0So when the life length Tx is random, the present value randomvariable isY a Tx 1 ν Tx.δIts present value is5-18

and its variance isdRecall that 1 Fx (t) t px and fx (t) dtt px . Also thatddat dtdt 1 νt ln(ν) νtTherefore, Za x E a Tx at t px0 Zat fx (t)dt 0Z ν t t px dt.0 at dt px dtdtint by parts05-19

It follows that5-20

Subsection 5.5.2 - Term Life Continuous AnnuityThe present value random variable for a term continuous annuitysetting ending at n (not necessarily an integer) years isY amin(Tx ,n) 1 ν min(Tx ,n),δSo its EPV isand its variance isVar [Y ] Var ν min(Tx ,n)δ2 2Ax:n 2 Ax:n δ2.Recall that Ax:n is the endowment EPV for life insurance. See pages4-20 and 4-21.5-21

Other expressions for the EPV includeZ ne δt t px dtax:n 0andZax:n 0n at t px µx t dt an n px .5-22

Example 5-5: Important Setting Assume a constant force of mortalityµ x and a constant force of interest δ. Find ax and ax:n .5-23

Example 5-6: Important Setting Assume a constant force of interestδ and a future life length that is de Moivre (0, ω x). Find ax andax:n .5-24

Section 5.6 - Annuities Payable mth lySubsection 5.5.1 - Whole Life Annuity Payable mth ly(m)(# of sub-periods survived)Here Kx and the payments are eachm1dollars,sothetotalpaymentovereachyear is 1.m5-25

For a whole life annuity-due setting, the present value randomvariable is(m)Y ä(m)(m)Kx1 m 1 ν (Kxd (m)1) m.The EPV is thenand the variance is (m) 1 Var ν (Kx m )Var [Y ] (d (m) )22 A(m)x (m) 2 Ax(d (m) )25-26

An alternative form for this EPV is Xk1(m)äx ν m k px .mmk 0For a whole life annuity-immediate, we see thatBecause their present value random variables differ only by aconstant, the variance expression for an annuity-immediate isidentical to the one for the annuity-due.5-27

Subsection 5.6.2 - Term Life Annuity Payable mth lyWhen payments cease after n years, the present value randomvariable of the annuity-due is:(m)Y ä(m)(m)min(Kx1 m,n)1 ν min(Kx d (m)1,n) m.So its EPV is:and its variance is (m)1Var ν min(Kx m ,n)Var [Y ] (d (m) )22 A(m)x:n (m) 2 Ax:n (d (m) )2(m)where Ax:n denotes an endowment EPV.5-28

An alternative form for the EPV is(m)äx:n mn 1X k 01m kνm km px .(m)We also note that the term annuity-immediate EPV, ax:n , is just like(m)äx:n except that it does not contain the constant first termand does contain a term at k mn, that is(m)ax:n mn X1k 1mkνm 1mat k 0 pkx .m5-29

In an annual annuity-due, a payment of 1 occurs at the beginning of1are made during the year, theythe year. When m payments are of mmove the mass (potential payments) further away from t 0. Thus,(m)äx äxfor m 1.Similar reasoning applied to an annuity-immediate shows that(m)ax axfor m 1.It follows that when m 1,The same relationships hold when comparing term annuity EPV’s.5-30

Example 5-7: Mortality follows de Moivre (0,80) for someone age x.If δ .05, find ax:20 .5-31

Example 5-8: If Y is the present value R.V. for someone age x, findE[Y ] whenY an when 0 Tx nandY aTx otherwise.5-32

Example 5-9: You are give that µ .01 and that δ .04 when0 t 5 and δ .03 when t 5. Find ax:10 .5-33

Example 5-10: Given δ .05 and µt .05 for 0 t 50 andµt .10 for t 50. Find the EPV of a 50 year temporary lifecontinuous payment annuity with 1 smeared over each year forinsured age 30, ceasing immediately at death.5-34

Example 5-11: A 30 year old will receive 5,000 annually beginningone year from today for as long as this person lives. When px k forall x, the actuarial PV of the annuity is 22,500, with i .10. Find k .5-35

1 .25 andExample 5-12: Given Ax .28, Ax 20 .40, Ax:20 i .05, find ax:20 .5-36

Section 5.8 - Deferred Life AnnuitiesA deferred life annuity does not begin payments until u years havepassed and then continues to make annual payments of 1 as long asthe annuitant is alive at the time of payment.Here Kx is the number of whole years survived by the annuitant, i.e.Kx bTx c. Also the distinction between an annuity-due and anannuity-immediate is moot in this setting. We could use either, butchoose to use annuity-due.5-37

LetYx ( 1 paid at the beginning of each year through Kx )andYx:u ( 1 paid at the beginning of each year through Kx ,with a maximum of u payments).The present value random variable for the deferred life annuity wouldthen beu Yx Yx Yx:u .It follows that the EPV is5-38

A second way to view a deferred whole life annuity is to consider itspayments year by potential year:u äx E[ u Yx ] 1 u px ν u 1 u 1 px ν u 1 1 u 2 px ν u 2 · · · u px ν u 1 1 1 px u ν 1 1 2 px u ν 2 · · · u px ν u äx uOnce again we see u Ex acting like a discount function. Similarly,when the annuity is a term (max of n payments) annuity,and for mth ly payment annuities (m)(m) ä Eäu xu xx u .5-39

Example 5-13: A continuous deferred annuity pays at a rate of(1.04)t at time t starting 5 years from now. You are given δ .07and µt .01 when t 5 and µt .02 when t 5. Find the actuarialpresent value of this annuity.5-40

Section 5.9 - Guaranteed AnnuitiesMoney accumulated in a 401K account is typically used to purchasea retirement annuity which will pay the annuitant a monthly incomefor the remainder of the annuitant’s life. These life annuities comewith guarantee options of 0, 5, 10, 15, or 20 years. The longer theguarantee period, the lower the monthly payment amounts, butthese decrements are usually not substantial.Consider an annual whole life annuity with a n-year guaranteeperiod, for which the annuitant is x years old. The present valuerandom variable of 1 annual payments is Y if Kx n 1än äKx 1 if Kx nwhere n Yx is the present value of a n-year deferred annualannuity-due.5-41

Thus the EPV of this n-year guaranteed annuity isäx:n E[ Y ] än E[ n Yx ]orWhen payments are made mth ly, the EPV becomes5-42

Example 5-14: Given Ax .3, Ax:20 .4, i .05 and 20 px .7, finda.x:20 5-43

Example 5-15: An annuity pays 1 at the beginning of each year for(35) and pays until age 65. Payments are certain for the first 15years. Calculate the EPV given: ä15 11.94, ä30 19.6,ä35:15 11.62, ä35:30 18.13, ä35 21.02, ä50 15.66 andä65 9.65 .5-44

Section 5.10 - Life Annuities With Increasing PaymentsSubsection 5.10.1 - Arithmetically Increasing AnnuitiesConsider the arithmetically increasing sequence of life contingentpayments pictured above. The EPV of these payments is5-45

If it is a term policy with n as the maximum number of annualpayments, then the EPV isIn general, suppose the arithmetically increasing sequence ofpayments is as shown below.5-46

The EPV in this general case is(P) äx (Q) 1 Ex (Iä)x 1 .With a continuous payment of t at time t, the EPV becomesIf the payments are a linear function of time, for example,Pt bt c, where b and c are constants, then the EPV isb Ia x cax .5-47