WIXLIB

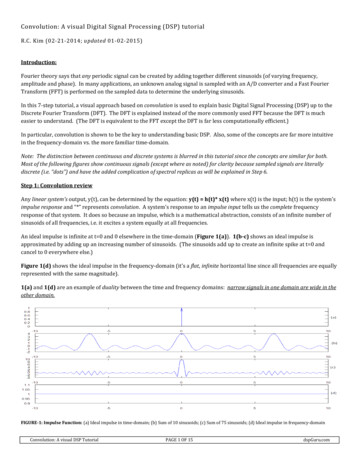
Micro-MeasurementsStrain Gages and InstrumentsTech Note TN-517Introduction to Digital Signal Processing1.0 IntroductionSampling rate: 1000/sWhen a signal varies with time, we are usually concernednot only with its magnitude but also with how it changes.Oscilloscopes, strip chart recorders and other analogrecording devices enable us to make observations ofthe signal by continuously recording and displaying themeasurement data in the time domain. When digitalcomputers are utilized for this purpose, however, themagnitude of the signal is sampled only at fixed intervalsof time with a complete loss of continuity between. Fordata acquired in this form, the mathematics of digitalsignal processing can be used to analyze the signal in boththe time and frequency domains. That is, we can know notonly how the magnitude of the signal varied with time, butalso what the amplitudes of any oscillations were over aspectrum of frequencies.This Tech Note is intended as a guide to understanding thenecessary considerations for converting an analog signalinto a useful series of discrete digital data, particularly asrelated to StrainSmart Data Systems.*ScansFrequency: 1000 Hz*01**23Time, msFigure 1Sampling rate: 1333/sFrequency: 1000 Hz2.0 Signal Aliasing2.1 FundamentalsCare must be taken when dealing with digital data toavoid the creation of false, lower-frequency signals by aphenomenon called aliasing. Do you remember seeing thespoke wheels of a wagon that appeared to turn backwardsas the wagon rolled across a television or movie screen?That’s a false visual impression caused by aliasing. Whenthe wheel is rotating at a slightly slower rate than that atwhich the frames are projected, the wheels appear to runin reverse. Further, if the wheels were rotated at the samerate as the frames are projected, the wheel would appear tobe static, or not turning at all!All sampling between 1000 and 2000 times per secondwould produce a lower-frequency alias. Shown here is the333-Hz alias that we would “see” at a sample rate of 1333per second (Figure 2).Document Number: 11067Revision: 01-Nov-2010Scans0***1.5Time, ms*3.0Figure 2Sampling at 2000 times per second, the signal would againappear to be static (Figure 3).So what is it that we must do to ensure that our instrumentalways sees the wagon wheel turning in the right direction?The answer is to always sample at more than twice thehighest rate of oscillation. When sampling at 4000 timesa second (Figure 4), we can see that it is impossible toproduce either a static or lower-frequency alias from themeasurements.For technical support, asurements.com169Tech NoteSimilar things can happen with an analog signal thatis sampled periodically. Consider a sinusoidal signaloscillating at, say, 1000 Hz, or 1000 times per second. Ifwe sample this signal at the same rate as the oscillations(Figure 1), we might think the signal was static, not varyingwith time.*

TN-517Micro-MeasurementsIntroduction to Digital Signal ProcessingSampling rate: 2000/s* Scans **01Frequency: 1000 Hz***2*3.0 Digital Filters3The sampling rate of the ADC is typically much higher thanthat required to extract the necessary information from thesignal within the frequency range of interest. In addition toallowing unwanted higher frequency components (noise)to remain in the data, these higher sampling rates will alsoincrease data storage requirements and analysis time.Time, msFigure 3Sampling rate: 4000/sprevented, it is necessary to remove all components ofthe signal and noise with frequencies of half or more thesampling rate with a low-pass anti-aliasing filter. This is ananalog circuit through which the input signal must pass onits way to the analog-to-digital converter. Of course, thefilter not only eliminates any aliasing in the digital data,but also attenuates any true signals — wanted or unwanted— above the stopband of the filter. Thus, when the data issubsequently analyzed with digital signal processing, weneed not worry about any false lower-frequency signalsbeing left in the data by the analog-to-digital conversionprocess.Frequency: 1000 HzIn preparation for acquiring data in digital form, theanalog signal being measured is typically passed throughan analog filter to ensure that all components of the signal,and noise with frequencies corresponding to a half, ormore, of the digital sampling rate of the analog-to-digitalconverter (ADC), are removed. As described in Section2.0, this helps ensure that false lower-frequency signals —called aliases — are not introduced into the digital data bythe sampling process itself.Scans*0* ** * * ** * * *12**3Time, msTech NoteFigure 4Just how fast should we sample? The mathematics usedin digital signal processing can construct a model of theanalog waveform that produced a particular set of databy looking at how the magnitudes of the measurementsdata vary over time. For frequency domain analysis, thesampling rate can be quite close to twice the maximumrate of oscillation. Reconstruction of the actual signalitself would require a sampling rate of ten or more timesthe highest frequency.2.2 Anti-aliasing FiltersIn the general case, we do not know the frequency of anyof the oscillations that might be present in the signal beingmeasured. But, as was just shown, we do know thoseof half or more the sampling rate will produce aliasesduring acquisition. Therefore, to ensure that aliases arewww.micro-measurements.com170In order to acquire data at a lower rate while avoidingaliasing errors, it would be necessary to make physicalchanges to the analog anti-aliasing filter and slow downthe sampling rate of the ADC. The disadvantage ofthis approach is that different analog filter componentsare required for each sampling rate. A more practicalsolution is to leave the analog filter and ADC sampling rateunchanged and to mathematically eliminate any unwantedcomponents from the measured signal by passing thedigital data through a digital filter.Specifically, low-pass digital filters enable the digitaldata coming from the ADC to be “decimated.” Insteadof the software processing and storing data from everyanalog-to-digital conversion, the digital filter allows datato be sampled at intervals corresponding to every n thconversion, effectively reducing the sampling rate withoutintroducing aliases. And, at the same time, any unwantedhigher frequency components of the measured signal areeliminated from the digital data as well.Like an analog filter, the digital filter is selected on thebasis of which frequencies in the signal are to be retainedand which are to be rejected. Low-pass filters, the mostcommon type, are designed to allow signal componentsFor technical questions, contactmicro-measurements@vishaypg.comDocument Number: 11067Revision: 01-Nov-2010

TN-517Micro-MeasurementsIntroduction to Digital Signal ProcessingPassbandRippleAttenuation, enuation0TransitionBandPassbandDigital FilterStopband0CutoffFrequencyAnalog Filter100FrequencyFigure 5When using digital filters, the user should pay attention toboth the stopband and the transition band. In some cases,particularly those with lower passband frequencies, theDocument Number: 11067Revision: 01-Nov-2010transition band may be as great as, or even greater than,the passband itself.Further, as shown in Figure 5, it should be noted that thepassband and stopband frequencies of digital filters differfrom the cutoff frequency of the commonly used Besseland Butterworth analog filters. The cutoff frequency of ananalog filter, typically specified at an attenuation of 3 dB,usually lies in the transition band between the passbandand stopband frequencies of com parable digital filters.Digital filters are a combination of mathematical algorithms and fast digital circuits that operate on a series ofdigital data acquired over a period of time. The necessityof using a series of data leads to a delay as the data passesFor technical questions, asurements.com171Tech Notefrom 0 Hz (dc) to some nonzero passband frequency, fo,to pass essentially un a ltered (Figure 5). The filter doesintroduce a series of small positive and negative deviationsfrom the actual signal in the passband. When this “ripple”exceeds a certain amount, typically 0.01 dB, it defines thepassband frequency. For frequencies in the transition bandbetween the passband frequency and higher stopbandfrequency, the signal is increasingly attenuated. When theattenuation reaches a certain level, typically in the vicinityof 95 dB, it defines the stopband frequency of the digitalfilter.